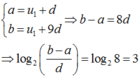công thức a là số hạng thứ bn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 8 2023
1; Số số hạng = (số cuối - số đầu) : khoảng cách + 1
2; tổng = (số cuối + số đầu)\(\times\) số số hạng : 2
3; số thứ n = khoảng cách \(\times\)(n-1) + số đầu
4 tìm số đó đứng thứ mấy
vị trí của số cần tìm: (số đó - số đầu): khoảng cách + 1
1 tháng 8 2023
1.SSH = ( SC - SĐ ) : KC + 1
2.T = ( SĐ + SC ) x SSH :2
3.STn = ( n - 1 ) x KC + SĐ
4. Số đó đứng thứ mấy = ( Số đó - SĐ ) : KC +1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Ta có:
\(\begin{array}{l}{u_1} + {u_2} + {u_3} = - 1 \Leftrightarrow {u_1} + {u_1} + d + {u_1} + 2d = - 1\\ \Leftrightarrow 3{u_1} + 3d = - 1\\ \Leftrightarrow 3.\left( {\frac{1}{3}} \right) + 3d = - 1\\ \Leftrightarrow 3d = - 2\\ \Leftrightarrow d = - \frac{2}{3}\end{array}\)
Công thức tổng quát của số hạng \({u_n}\): \({u_n} = \frac{1}{3} + \left( {n - 1} \right)\left( { - \frac{2}{3}} \right)\)
b) Ta có:
\(\begin{array}{l} - 67 = \frac{1}{3} + \left( {n - 1} \right).\left( { - \frac{2}{3}} \right)\\ \Leftrightarrow n - 1 = 101\\ \Leftrightarrow n = 102\end{array}\)
- 67 là số hạng thứ 102 của cấp số cộng
c) Ta có:
\(\begin{array}{l}7 = \frac{1}{3} + \left( {n - 1} \right).\left( { - \frac{2}{3}} \right)\\ \Leftrightarrow n - 1 = - 10\\ \Leftrightarrow n = - 9\end{array}\)
7 không là số hạng của cấp số cộng
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Ta có: \({u_n} = - 3 + \left( {n - 1} \right).5\)
b) Ta có:
\(\begin{array}{l}492 = - 3 + \left( {n - 1} \right).5\\ \Leftrightarrow n - 1 = 99\\ \Leftrightarrow n = 100\end{array}\)
492 là số hạng thứ 100 của cấp số cộng
c) Ta có: \(300 = - 3 + \left( {n - 1} \right).5 \Leftrightarrow n - 1 = 60,6\)
300 không là số hạng của cấp số cộng
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \({u_2} = {u_1}.q\)
\({u_3} = {u_2}.q = {u_1}.{q^2}\)
\({u_4} = {u_3}.q = {u_1}.{q^3}\)
\({u_5} = {u_4}.q = {u_1}.{q^4}\)
b) Từ a suy ra: \({u_n} = {u_1} \times {q^{n - 1}}\).
