Cho hình thang ABCD vuông tại A, đáy nhỏ AB.Cmr: a) AC>BD b) AC2 - BD2 =CD2 - AB2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-Sửa đề: \(\widehat{A}=\widehat{D}=90^0\)
a) -△OAB và △OCD có: \(\widehat{OAB}=\widehat{OCD};\widehat{AOB}=\widehat{COD}\)
\(\Rightarrow\)△OAB∼△OCD (g-g).
b) \(AC^2-BD^2=DC^2-AB^2\)
\(\Leftrightarrow AC^2-DC^2=BD^2-AB^2\)
\(\Leftrightarrow AD^2=AD^2\) (luôn đúng).
c) -△BCD có: OI//DC \(\Rightarrow\dfrac{DC}{OI}=\dfrac{BD}{BO}\Rightarrow\dfrac{DC}{OI}-1=\dfrac{OD}{BO}\)
-△AOB có: AB//DC \(\Rightarrow\dfrac{OD}{BO}=\dfrac{DC}{AB}=\dfrac{DC}{OI}-1\)
\(\Rightarrow\dfrac{DC}{AB}+1=\dfrac{DC}{OI}\Rightarrow\dfrac{DC+AB}{AB}=\dfrac{DC}{OI}\Rightarrow\dfrac{1}{OI}=\dfrac{DC+AB}{DC.AB}=\dfrac{1}{AB}+\dfrac{1}{DC}\)

Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)

a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
b: \(BD=\sqrt{3^2+4^2}=5\left(cm\right)\)
ΔOAB đồng dạng với ΔOCD
=>OB/OD=AB/DC=1/2
=>OB/1=OD/2=5/3
=>OB=5/3cm; OD=10/3cm

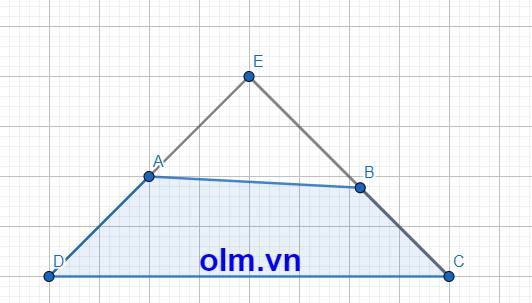
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)

a, Vì ABID và ABCK là hbh nên \(AB=DI;AB=CK\)
Do đó \(DI=CK\Rightarrow DI-KI=CK-KI\)
Vậy \(KD=CI\)
b, Áp dụng Talet: \(\dfrac{DE}{EB}=\dfrac{DK}{AB}=\dfrac{CI}{AB}=\dfrac{IF}{FB}\left(DK=CI\right)\)
Suy ra EF//CD (Talet đảo)
Áp dụng Talet: \(\dfrac{AB}{EF}=\dfrac{DI}{EF}=\dfrac{BD}{BE}=\dfrac{BE+ED}{BE}=1+\dfrac{ED}{BE}=1+\dfrac{DK}{AB}=1+\dfrac{CD-CK}{AB}=1+\dfrac{CD-AB}{AB}=\dfrac{CD}{AB}\)
Vậy \(AB^2=EF\cdot CD\)
ta có \(AC=\sqrt{AD^2+DC^2}>\sqrt{AD^2+BA^2}=DB\) vậy AC>BD
. từ trên ta có :
\(\hept{\begin{cases}AC^2=AD^2+DC^2\\BD^2=AD^2+BA^2\end{cases}\Rightarrow AC^2-BD^2=CD^2-AB^2}\)