Tìm các giá trị nguyên của x để phân thức M có giá trị là một số nguyên
M=\(\frac{10x^2-7x-5}{2x-3}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 6 2021
`M=(10x^2-7x-5)/(2x-3)(x ne 3/2)`
`=(10x^2-15x+8x-12+7)/(2x-3)`
`=(5x(2x-3)+4(2x-3)+7)/(2x-3)`
`=5x+4+7/(2x-3)`
Để `M in ZZ`
`=>7/(2x-3) in ZZ`
`=>2x-3 in Ư(7)={+-1,+-7}`
`=>2x in {2,4,-4,10}`
`=>x in {1,2,-2,5}(tm)`
Vậy `x in {1,2,-2,5}` thì `M in ZZ`.
AA
4
30 tháng 6 2015
\(M=\frac{10x^2-15x+8x-12+7}{2x-3}=\frac{\left(2x-3\right)\left(5x+4\right)+7}{2x-3}=5x+4+\frac{7}{2x-3}\)
=> M nguyên <=> 5x+4 nguyên và 7/2x-3 nguyên <=> x nguyên và 2x-3 thuộc Ư(7) <=> 2x-3 thuộc (+-1; +-7)
| 2x-3 | 1 | -1 | 7 | -7 |
| x | 2(t/m đk) | 1(t/m đk) | 5(t/mđk) | -2(t/m đk) |
=> M nguyên <=> x thuộc (-2;1;2;5)
5 tháng 11 2017
Ví dụ : Tìm tập hợp các ước của 24
Ư(24) = {1 ; 2 ; 3 ; 4 ; 6 ; 8 ; 12 ; 24 }
Ta có thể tìm các ước của a bằng cách lần lượt chia a cho
các số tự nhiên từ 1 đến a để xét xem a chia hết cho những
số nào ,khi đó các số ấy là ước của a
GV
Giáo viên Toán
Giáo viên
24 tháng 4 2017
Biến đổi M về dạng \(M=f\left(x\right)+\dfrac{n}{2x-3}\) như sau:
Cách 1: chia đa thức \(10x^2-7x-5\) cho \(2x-3\) ta được thương là \(5x+4\) dư là 7. Vậy:
\(M=5x+4+\dfrac{7}{2x-3}\)
Cách 2: Biến đổi M như sau:
\(M=\dfrac{10x^2-7x-5}{2x-3}=\dfrac{10x^2-15x+8x-12+7}{2x-3}\)
\(=\dfrac{5x\left(2x-3\right)+4\left(2x-3\right)+7}{2x-3}\)
\(=5x+4+\dfrac{7}{2x-3}\)
Sau đó các bước tiếp theo làm như bạn Nhật Linh.
PT
1
CM
29 tháng 4 2019
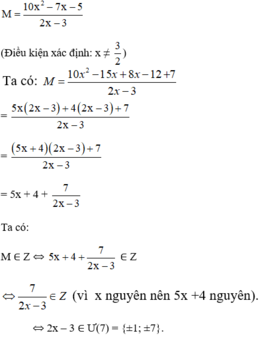
+ 2x – 3 = 1 ⇔ 2x = 4 ⇔ x = 2.
+ 2x – 3 = -1 ⇔ 2x = 2 ⇔ x = 1.
+ 2x – 3 = 7 ⇔ 2x = 10 ⇔ x = 5
+ 2x – 3 = -7 ⇔ 2x = -4 ⇔ x = -2.
Vậy với x ∈ {-2; 1; 2; 5} thì giá trị biểu thức M là một số nguyên.
NM
1
24 tháng 4 2017
Ta có \(M=\frac{10x^2-7x-5}{2x-3}=5x+4+\frac{7}{2x-3}\)
Để \(M=5x+4+\frac{7}{2x-3}\) là số nguyên <=> \(\frac{7}{2x-3}\)là số nguyên
\(\Rightarrow7⋮2x-3\) hay \(2x-3\inƯ\left(7\right)\)
\(\RightarrowƯ\left(7\right)=\) { - 7; - 1; 1; 7 }
Ta có : 2x - 3 = 7 <=> 2x = 10 => x = 5 (t/m)
2x - 3 = 1 <=> 2x = 4 => x = 2 (t/m)
2x - 3 = - 1 <=> 2x = 2 => x = 1 (t/m)
2x - 3 = - 7 <=> 2x = - 4 => x = - 2 (t/m)
Vậy với x \(\in\) { - 2; 1; 2; 5 } thì M là số nguyên
27 tháng 12 2020
a) ĐKXĐ: \(x\notin\left\{3;-3;-2\right\}\)
Ta có: \(P=\left(\dfrac{2x-1}{x+3}-\dfrac{x}{3-x}-\dfrac{3-10x}{x^2-9}\right):\dfrac{x+2}{x-3}\)
\(=\left(\dfrac{\left(2x-1\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{3-10x}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{x+2}{x-3}\)
\(=\dfrac{2x^2-6x-x+3+x^2+3x-3+10x}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+2}{x-3}\)
\(=\dfrac{3x^2+6x}{\left(x-3\right)\left(x+3\right)}:\dfrac{x+2}{x-3}\)
\(=\dfrac{3x\left(x+2\right)}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{x+2}\)
\(=\dfrac{3x}{x+3}\)
b) Ta có: \(x^2-7x+12=0\)
\(\Leftrightarrow x^2-3x-4x+12=0\)
\(\Leftrightarrow x\left(x-3\right)-4\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(loại\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
Thay x=4 vào biểu thức \(P=\dfrac{3x}{x+3}\), ta được:
\(P=\dfrac{3\cdot4}{4+3}=\dfrac{12}{7}\)
Vậy: Khi \(x^2-7x+12=0\) thì \(P=\dfrac{12}{7}\)
GA
25 tháng 2 2020
\(M+\frac{2x^2}{\left(3-x\right)\left(x+1\right)}=\frac{2x}{\left(x-1\right)\left(x+1\right)}+\frac{4x}{\left(3-x\right)\left(x+1\right)}\)
\(M=\frac{2x}{\left(x-1\right)\left(x+1\right)}+\frac{4x}{\left(3-x\right)\left(x+1\right)}-\frac{2x^2}{\left(3-x\right)\left(x+1\right)}\)
\(M=\frac{2x\left(3-x\right)}{\left(3-x\right)\left(x-1\right)\text{}\left(x+1\right)}+\frac{4x\left(x-1\right)}{\left(3-x\right)\left(x-1\right)\left(x+1\right)}+\frac{2x^2\left(x-1\right)}{\left(3-x\right)\left(x-1\right)\left(x+1\right)}\)
\(M=\frac{6x-2x^2+4x^2-4x+2x^3-2x^2}{\left(3-x\right)\left(x-1\right)\left(x+1\right)}\)
\(M=\frac{2x^3-2x}{\left(3-x\right)\left(x-1\right)\left(x+1\right)}\)
\(M=\frac{2x\left(x-1\right)}{\left(3-x\right)\left(x-1\right)\left(x+1\right)}\)
\(M=\frac{2x}{\left(3-x\right)\left(x+1\right)}\)
có gì sai sót bạn bỏ qua
Học tốt
\(\text{Để }\frac{10x^2-7x-5}{2x-3}nguyên\Rightarrow\left(10x^2-7x-5\right)⋮\left(2x-3\right)\)
\(\text{Ta có }10x^2-7x-5=10x^2-7x-12+7=\left(2x-3\right)\left(5x+4\right)+7\)\(Mà\left(2x-3\right)\left(5x+4\right)⋮\left(2x-3\right)\Rightarrow7⋮\left(2x-3\right)\)
\(\Rightarrow\left(2x-3\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\text{Vậy x }\in\left\{-2;1;2;5\right\}\)