Giúp câu 17, 19 vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
DT
Đỗ Thanh Hải
CTVVIP
24 tháng 5 2021
17 do you
18 shouldn't they
19 does she
20 can't he
21 will you
22 shouldn't they
23 does she
24 can they
25 doesn't it
24 tháng 5 2021
17 do you
18 shouldn't they
19 does she
20 can't he
21 will you
22 shouldn't they
23 does she
24 can they
25 doesn't it
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2022
16.
\(\lim\dfrac{u_n}{v_n}=+\infty\)
17.
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AB\Rightarrow\Delta SAB\) vuông tại A (B đúng)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\) (C đúng)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\) (D đúng)
18.
Tập hợp điểm cách đều 2 điểm AB cho trước là mặt phẳng trung trực của AB
19.
\(\lim\limits_{x\rightarrow1}\dfrac{x-1}{2x-2}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{2\left(x-1\right)}=\dfrac{1}{2}\)
TH
1
VT
9 tháng 3 2022
6. B
7. D
8. C
9. A
10. A
11. A
12. A
13. A
14. B
15. C
16. B
17. C
18. A
19. C
25 tháng 8 2021
Câu 19 : Phép đối xứng qua tâm M biến đường tròn (O;R) thành đường tròn (O' ; R)
=> Đường tròn này cố định
H thuộc đường tròn này đấy. CM thì dùng Kiến thức lớp 9 ấy. Thế nhá
MC
1
29 tháng 6 2023
28D
27: Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}a\cdot2+b=3\\a\cdot\left(-1\right)+b=0\end{matrix}\right.\Leftrightarrow a=1\)
=>Chọn A
43:
tọa độ A là;
y=0 và x+3=0
=>A(-3;0)
Tọa độ B là;
-x+3=0 và y=0
=>B(3;0)
Tọa độ C là;
x+3=-x+3 và y=x+3
=>x=0 và y=3
=>C(0;3)
A(-3;0); B(3;0); C(0;3)
\(AB=\sqrt{\left(3+3\right)^2+\left(0-0\right)^2}=6\)
\(AC=\sqrt{\left(0+3\right)^2+\left(3-0\right)^2}=3\sqrt{2}\)
BC=căn (0-3)^2+(3-0)^2=3*căn 2(cm)
Vì BC^2+AC^2=AB^2 và BC=AC
nên ΔABC vuông cân tại B
P=1/2(3căn 2+3căn 2+6)=3căn 2+3(cm)
S=1/2*3*căn 2*3*căn 2=9
=>r=9/3căn 2+3=-3+3căn 2=1,243
=>Chọn D
AW
2
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
17.
Gọi số vi khuẩn ban đầu là x
Sau 5 phút số vi khuẩn là: \(x.2^5=64000\Rightarrow x=2000\)
Sau k phút:
\(2000.2^k=2048000\Rightarrow2^k=1024=2^{10}\)
\(\Rightarrow k=10\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
18.
\(S_{2019}=\left(\dfrac{1}{2}\right)^1+1+\left(\dfrac{1}{2}\right)^2+1+...+\left(\dfrac{1}{2}\right)^{2019}+1\)
\(=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}+2019\)
Xét \(S=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}\) là tổng cấp số nhân với \(\left\{{}\begin{matrix}u_1=\dfrac{1}{2}\\q=\dfrac{1}{2}\\n=2019\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{1}{2}.\dfrac{\left(\dfrac{1}{2}\right)^{2019}-1}{\dfrac{1}{2}-1}=1-\dfrac{1}{2^{2019}}\)
\(\Rightarrow S_{2020}=2019+S=2020-\dfrac{1}{2^{2019}}\)
19. C là khẳng định sai, ví dụ: \(u_n=2\) ; \(v_n=-\dfrac{1}{n}\)
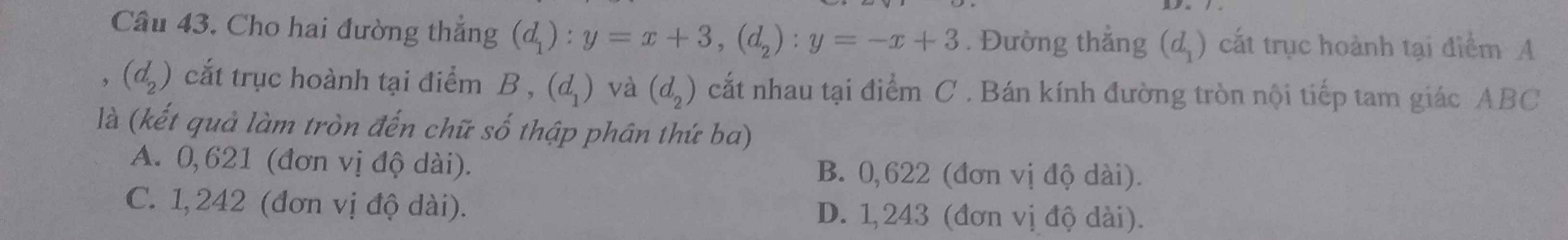
17.
Câu 17 này đề bài sai (ở độ dài AB, nếu ko nhìn lầm thì AB=41 là 1 con số phi lý)
Cách tính như sau:
Qua \(C_1\) kẻ các đường thẳng song song AC và BC, cắt \(AA_1\) và \(BB_1\) kéo dài tại D và E
\(\Rightarrow ABC.DEC_1\) là lăng trụ đứng có thể tích V
\(V=CC_1.S_{ABC}=6.\dfrac{AB^2\sqrt{3}}{4}=\dfrac{3AB^2\sqrt{3}}{2}\)
Gọi thể tích khối đa diện cần tính là \(V_1\)
\(\Rightarrow\dfrac{V_1}{V}=\dfrac{1}{3}\left(\dfrac{AA_1}{AD}+\dfrac{BB_1}{BE}+\dfrac{CC_1}{CC_1}\right)=\dfrac{5}{6}\)
\(\Rightarrow V_1=\dfrac{5}{6}V=...\)
Hình vẽ câu 17: