Chứng minh với α là góc nhọn tùy ý
a, Cos4 α - Sin4 α = 1 - 2Sin2 α
b, 1 + tan2 α = 1/Cos2 α
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
12 tháng 12 2019
Chọn D.
Ta có P = ( sin2α - cos2α) ( sin2α + cos2α) = sin2α - cos2α (*)
Chia hai vế của (*) cho cos2 α ta được 
Tương đương: P(1 + tan2α) = tan2α - 1
CM
18 tháng 9 2019
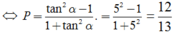
Ta có:
C = sin 4 α + cos 4 α = sin 4 α + cos 4 α + 2 sin 2 α . cos 2 α - 2 sin 2 α . cos 2 α
= sin 2 α + cos 2 α 2 - 2 sin 2 α . cos 2 α
= 1 - 2 sin 2 α . cos 2 α ( v ì sin 2 α + cos 2 α = 1 )
Vậy C = 1 - 2 sin 2 α . c o s 2
Đáp án cần chọn là: A
29 tháng 10 2021
a: \(=\left(\sin^2\alpha+\cos^2\alpha\right)^2=1^2=1\)
CM
10 tháng 10 2019
Chọn B.
Theo giả thiết ta có: 3sin4 α – cos4 α = ½. Nên 3sin4 α – (1- sin2 α)2 = ½.
Hay 6sin4α - 2(1 - 2sin2α + sin4α) = 1
Suy ra: 4sin4α + 4sin2α - 3 = 0
Nên sin2α = 1/2
Ta lại có cos2α = 1 - sin2α = 1 - 1/2 = ½
Suy ra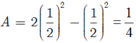 
TA
14 tháng 6 2021
VT `=1+tan^2 α`
`=1+ (sin^2α)/(cos^2α)`
`= (cos^2α+sin^2α)/(cos^2α)`
`= 1/(cos^2α)`
14 tháng 6 2021
a, \(1+tan^2a=\dfrac{1}{\cos^2a}\)
ĐT \(\Leftrightarrow\cos^2a\left(1+\tan^2a\right)=1\)
\(\Leftrightarrow\cos^2a+\cos^2a.\tan^2a=1\)
\(\Leftrightarrow\cos^2a.\dfrac{\sin^2a}{\cos^2a}+\cos^2a=\sin^2a+\cos^2a=1\) ( ĐT đã có )
=> ĐPCM
Vậy ...
CM
24 tháng 3 2017
Áp dụng định lí pitago trong tam giác vuông OAB có:
OB2 = OA2 + AB2
Từ đó ta có:
28 tháng 6 2021
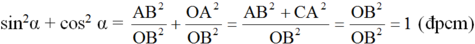
\(sin\alpha^2+cos\alpha^2=1\Rightarrow sin\alpha^2=1-cos\alpha^2=1-\dfrac{1}{25}=\dfrac{24}{25}\Rightarrow sin\alpha=\dfrac{2\sqrt{6}}{5}\)
\(\Rightarrow cot\alpha=\dfrac{cos\alpha}{sin\alpha}=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{24}\)
28 tháng 6 2021
\(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\sin^2\alpha=1-\dfrac{1}{25}=\dfrac{24}{25}\)
hay \(\sin\alpha=\dfrac{2\sqrt{6}}{5}\)
\(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{2\sqrt{6}}{5}:\dfrac{1}{5}=2\sqrt{6}\)
\(\cot\alpha=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)
a) ta có \(VT=cos^4\alpha-sin^4\alpha=\left(cos^4\alpha+sin^4\alpha\right)-2sin^4\alpha\)
\(=\left(\left(sin^2\alpha+cos^2\alpha\right)^2-2sin^2\alpha.cos^2\alpha\right)-2sin^4\alpha\)
\(=1-2sin^2\alpha.cos^2\alpha-2sin^4\alpha=1-2sin^2\alpha\left(cos^2\alpha+sin^2\alpha\right)\)
\(=1-2sin^2\alpha=VP\left(đpcm\right)\)
b) ta có : \(VP=\dfrac{1}{cos^2\alpha}=\dfrac{sin^2\alpha+cos^2\alpha}{cos^2\alpha}=1+tan^2\alpha=VT\left(đpcm\right)\)