cho hàm số : y = √x−m+√2x−m−1x−m+2x−m−1 . tìm m để hàm số đã cho xác định trên tập số D và chứa mọi x > 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2021
b: để hai đường cắt nhau tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m^2-7=2\\m-1< >2\end{matrix}\right.\Leftrightarrow m=-3\)
8 tháng 2 2021
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
8 tháng 2 2021
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
14 tháng 7 2021
Bài 1:
a) Để hàm số y=(k-2)x+k+3 là hàm số bậc nhất thì \(k\ne2\)
b) Để hàm số y=(k-2)x+k+3 đồng biến trên R thì k-2>0
hay k>2
Bài 2:
Thay \(x=-\dfrac{1}{2}\) và \(y=\dfrac{2}{3}\) vào (D), ta được:
\(\left(2m-3\right)\cdot\dfrac{-1}{2}-\dfrac{1}{2}=\dfrac{2}{3}\)
\(\Leftrightarrow\left(2m-3\right)\cdot\dfrac{-1}{2}=\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}\)
\(\Leftrightarrow2m-3=\dfrac{7}{6}:\dfrac{-1}{2}=\dfrac{-7}{6}\cdot\dfrac{2}{1}=-\dfrac{14}{6}=-\dfrac{7}{3}\)
\(\Leftrightarrow2m=\dfrac{-7}{3}+3=\dfrac{-7}{3}+\dfrac{9}{3}=\dfrac{2}{3}\)
hay \(m=\dfrac{1}{3}\)
CM
12 tháng 1 2017
Chọn đáp án D
Hàm số xác định khi
Do đó hàm số đã cho xác định trên 0 ; + ∞
CM
19 tháng 5 2017
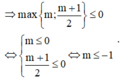
Đáp án A
T X D : D = ℝ \ 1
Ta có: y = m x 2 − m + 2 x + m 2 − 2 m + 2 x − 1 = m x − 2 + m 2 − 2 m x − 1 ⇒ y ' = m − m 2 − 2 m x − 1 2
hàm số luôn đồng biến trên tập xác định của nó khi y ' ≥ 0 ∀ x ∈ D (dấu bằng xảy ra tại hữu hạn điểm)
⇔ m − m 2 − 2 m x − 1 2 ≥ 0 ∀ x ∈ D ⇔ x x − 1 2 ≥ m 2 − 2 m ∀ x ∈ D
Với m = 0 ⇒ y ' = 0 ∀ x ∈ D (không thỏa mãn dấu bằng xảy ra tại hữu hạn điểm)
Khi đó hàm số luôn đồng biến trên tập xác định m > 0 m 2 − 2 m ≤ 0 ⇔ 0 < m ≤ 2
26 tháng 12 2020
2) Để (d) đi qua A(2;8) thì Thay x=2 và y=8 vào hàm số \(y=\left(m^2-2m+3\right)x-4\), ta được:
\(\left(m^2-2m+3\right)\cdot2-4=8\)
\(\Leftrightarrow2m^2-4m+6-4-8=0\)
\(\Leftrightarrow2m^2-4m-6=0\)
\(\Leftrightarrow2m^2-6m+2m-6=0\)
\(\Leftrightarrow2m\left(m-3\right)+2\left(m-3\right)=0\)
\(\Leftrightarrow\left(m-3\right)\left(2m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-3=0\\2m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\2m=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Vậy: Để (d) đi qua A(2;8) thì \(m\in\left\{3;-1\right\}\)