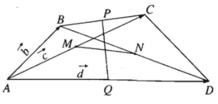
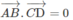Cho tứ giác ABCD có AC = BD. Gọi M, E, N lần lượt là trung điểm của AD, DC và BC.
a) Chứng minh \(\widehat{EMN}=\widehat{ENM}\)
b) Chúng minh \(MN\le\frac{AB+CD}{2}\)
c) Chứng minh nếu \(MN=\frac{AB+CD}{2}\)thì ABCD là hình thang.
( Lưu ý: Không sử dụng kiến thức về đường trung bình của hình thang, chỉ dùng kiến thức đường trung bình của hình tam giác )