Nghiệm nguyên nhỏ nhất của bất phương trình : \(\sqrt{x+1}< x+3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
NK
31 tháng 3 2020
a)11x-7<8x+7
<-->11x-8x<7+7
<-->3x<14
<--->x<14/3 mà x nguyên dương
---->x \(\in\){0;1;2;3;4}
NK
31 tháng 3 2020
b)x^2+2x+8/2-x^2-x+1>x^2-x+1/3-x+1/4
<-->6x^2+12x+48-2x^2+2x-2>4x^2-4x+4-3x-3(bo mau)
<--->6x^2+12x-2x^2+2x-4x^2+4x+3x>4-3+2-48
<--->21x>-45
--->x>-45/21=-15/7 mà x nguyên âm
----->x \(\in\){-1;-2}
MN
1
17 tháng 7 2016
\(\sqrt{x}>2\) (ĐKXĐ: \(x\ge0\))
\(\Leftrightarrow x>4\). Vì x là số nguyên nhỏ nhất nên x = 5 thoả mãn bất phương trình.
FA
1
CM
29 tháng 7 2018
Chọn A
Điều kiện: -1< x< 1.
Ta có:
Bất phương trình đã cho tương đương:
log3( 1-x2) ≤ - log3(1-x) hay log3( 1-x2) + log3( 1-x)≤ 0.
=> log3[ ( 1-x2).( 1-x)]
=> (1-x2)( 1-x)≤ 1 ó 1-x-x2+ x3 ≤ 1
ó x3-x2- x≤ 0
ó x
Kết hợp với điều kiện; suy ra x=0 là nghiệm nguyên nhỏ nhất của bất phương trình..
Chọn A.
NT
23 tháng 2 2016
pt<=>\(\sqrt{x^2-16x+64-58}\)=\(\sqrt{\left(x-8\right)^2+58}\)
=> gtnn= \(\sqrt{58}\)
khi x=8
3 tháng 10 2016
1/ \(\frac{3}{2}x^2+y^2+z^2+yz=1\Leftrightarrow3x^2+2y^2+2z^2+2yz=2\)
\(\Leftrightarrow\left(x^2+y^2+z^2+2xy+2yz+2zx\right)+\left(x^2-2xy+y^2\right)+\left(x^2-2zx+z^2\right)=2\)
\(\Leftrightarrow\left(x+y+z\right)^2+\left(x-y\right)^2+\left(x-z\right)^2=2\)
\(\Rightarrow-\sqrt{2}\le x+y+z\le\sqrt{2}\)
Suy ra MIN A = \(-\sqrt{2}\)khi \(x=y=z=-\frac{\sqrt{2}}{3}\)
3 tháng 8 2015
=> 2x2 + 2x - x2 + 3x -6 < 0
=> x2 + 5x - 6 < 0
=> x2 -x + 6x - 6 < 0 => x(x - 1) + 6(x -1) < 0 => (x+6).(x -1) < 0
=> x+ 6 và x - 1 trái dấu
Mà x + 6 > x - 1 nên x + 6 > 0 và x - 1< 0
=> x > -6 và x < 1
hay -6 < x < 1
Vậy nghiệm của bất pt là -6 < x < 1
TN
1
29 tháng 7 2016
\(\sqrt{4x-1}\ge4\)
<=> \(\begin{cases}4x-1\ge0\\4x-1\ge16\end{cases}\)
<=>x>=1/4=> ngiệm nguyên nhỏ nhất là L: 1
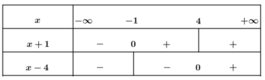
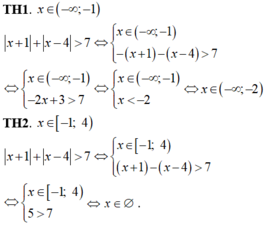
điều kiện : \(x\ge-1\)
ta có : \(\sqrt{x+1}< x+3\Leftrightarrow x+1< x^2+6x+9\)
\(\Leftrightarrow x^2+5x+8>0\Leftrightarrow x\in R\)
kết hợp với điều kiện \(\Rightarrow x\ge-1\)
vậy nghiệm nguyên nhỏ nhất của bất phương trình trên là \(x=-1\)