Question

[Nguyễn Vũ Đăng Trọng]

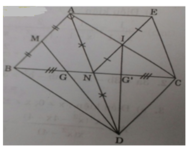
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Lấy E đối xứng với P qua N.

a) Chứng minh: Tứ giác AECP là hình thoi.

b)Cho MH cắt đường thẳng AE tại F. Chứng minh: Tứ giác AHBF là hình chữ nhật.

c) Chứng minh: MN, AP, và BE đồng quy.

d) Tìm điều kiện để tứ giác ECHF là hình bình hành.

Answer 1

[Nguyễn Lê Phước Thịnh]

a: Xét tứ giác APCE có

N là trung điểm chung của AC và PE

nên APCE là hình bình hành

mà PA=PC

nênAPCE là hình thoi

b: Xét ΔMAF và ΔMBH có

góc AMF=góc HMB

MA=MB

góc MAF=góc MBH

Do đó: ΔMAF=ΔMBH

Suy ra: MF=MH

Xét tứ giác AHBF có

M là trung điểm chung của AB và HF

nên AHBF là hình bình hành

mà góc AHB=90 độ

nên AHBF là hình chữnhật

c: Xét ΔABC có

N là trung điểm của AC

P là trung điểm của BC

Do đó: NP là đường trung bình

=>NP//AB và NP=AB/2

=>NP//AM và NP=AM

=>AMPN là hình bình hành

=>AP cắtMN tại trung điểm của mỗi đường(2)

Xét tứ giác AEPB có

PE//AB

PE=AB

Do đó: AEPB là hình bình hành

Suy ra: AP cắt EB tại trung điểm của mỗi đườg(1)

Từ (1) và (2) suy ra AP,EB,NM đồng quy