Cho đường tròn tâm O bán kính R và hai điểm cố định A và B. Với mỗi điểm M ta xác định điểm M' sao cho \(\overrightarrow{MM'}=\overrightarrow{MA}+\overrightarrow{MB}\) Khi M di động trên đường tròn tâm (O;R). Tìm tập hợp điểm M'.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc OMA+góc ONA=180 độ
=>OMAN nội tiếp
b: AM=căn 9a^2-4a^2=a*căn 5
S AMON=2*S AMO=AM*MO=2a^2*căn 5

Xét (O'): \(O'A\perp AB\) tại A và O'A là bán kính.
\(\Rightarrow\)AB là tiếp tuyến của (O') tại A.
\(\Rightarrow\widehat{NAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AN.
Mặt khác \(\widehat{AMN}\) là góc nội tiếp chắn cung AN.
\(\Rightarrow\widehat{AMN}=\widehat{NAB}\left(1\right)\)
Xét (O): \(\widehat{AMC}=\widehat{ABC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\widehat{NAB}=\widehat{ABC}\) nên AN//BC.

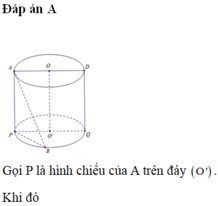
Đáp án A
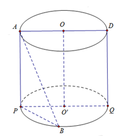
Gọi P là hình chiếu của A trên đáy O ' . Khi đó
A B = A P 2 + P B 2 = h 2 + B P 2 = 4 R 2 + P B 2 ≤ 4 R 2 + 4 R 2 = 2 R 2
Dấu bằng xảy ra ⇔ B P = P Q = 2 R .