CMR
8^12-2^23-2^30 chia hết cho 220
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


CMR : a)n(n^2+12)+(2_ngày)(n^2_3n+1)(n^2_3n+1)+8 chia hết cho 5 với mọi n thuộc Z
b)n^5_n chia hết cho 30
Ta có: 30=5.6, mà (5;6)=1 nên ta chứng minh n5-n chia hết cho 5 và 6
+) n5-n=n(n4-1)=n(n2-1)(n2+1)=n(n-1)(n+1)(n2-4+5)=n(n-1)(n+1)(n2-4)+5n(n-1)(n+1)
=(n-2)(n-1)n(n+1)(n+2)+5n(n-1)(n+1)
Vì (n-2)(n-1)n(n+1)(n+2) là tích của 5 số nguyên liên tiếp nên chia hết cho 5
5n(n-1)(n+1) chia hết cho 5
=> n5-n chia hết cho 5 (1)
+) n5-n=n(n4-1)=n(n2-1)(n2+1)=n(n-1)(n+1)(n2+1)
=(n-1)n(n+1)(n2+1)
Vì (n-1)n(n+1) là tích của 3 số nguyên liên tiếp nên chia hết cho 6
=> (n-1)n(n+1)(n2+1) chai hết cho 6
=> n5-n chia hết cho 6 (2)
Từ (1) và (2) => n5-n chia hết cho 30
Vậy n5-n chia hết cho 30 (đpcm)

a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:

![]()
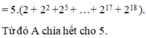

b) A=2+22+23+...+220
A=(2+22)+(23+24)+...+(219+220)
A=3.2+3.23+...+3.219
A=3.(2+23+25+...+219)
⇒A⋮3
phần c) làm tương tự

a) \(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(A=2\cdot\left(1+3\right)+2^3\cdot\left(1+3\right)+...+2^{59}\cdot\left(1+3\right)\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\)
Vậy A chia hết cho 3
________
\(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\)
Vậy A chia hết cho 5

a: Ta có: \(A=2+2^2+2^3+...+2^{20}\)
\(=2\left(1+2+2^2+...+2^{19}\right)⋮2\)
b: Ta có: \(A=2+2^2+2^3+...+2^{20}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{19}\left(1+2\right)\)
\(=3\cdot\left(2+2^3+...+2^{19}\right)⋮3\)

a: \(G=8^8+2^{20}\)
\(=2^{24}+2^{20}\)
\(=2^{20}\left(2^4+1\right)=2^{20}\cdot17⋮17\)
b: Sửa đề: \(H=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\left(1+2\right)\)
\(=3\left(2+2^3+...+2^{59}\right)⋮3\)
\(H=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\left(2+2^4+...+2^{58}\right)⋮7\)
\(H=2+2^2+2^3+...+2^{60}\)
\(=\left(2+2^2+2^3+2^4\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2\left(1+2+2^2+2^3\right)+...+2^{57}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+...+2^{57}\right)⋮15\)
c: \(E=\left(1+3+3^2\right)+3^3\left(1+3+3^2\right)+...+3^{1989}\left(1+3+3^2\right)\)
\(=13\left(1+3^3+...+3^{1989}\right)⋮13\)
\(E=1+3+3^2+3^3+...+3^{1991}\)
\(=\left(1+3+3^2+3^3+3^4+3^5\right)+\left(3^6+3^7+3^8+3^9+3^{10}+3^{11}\right)+...+3^{1986}+3^{1987}+3^{1988}+3^{1989}+3^{1990}+3^{1991}\)
\(=364\left(1+3^6+...+3^{1986}\right)⋮14\)
Sửa đề: \(8^{12}-2^{33}-2^{30}\)
\(=2^{36}-2^{33}-2^{30}\)
\(=2^{30}\left(2^6-2^3-1\right)\)
\(=2^{30}\cdot55=2^{28}\cdot220⋮220\)