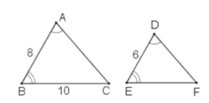
Cho Tam giác ABC tâm giác DEF, trong đó AB 6,5cm, góc D 70độ, AC 8cm. Tính DE, góc A,DF Giúp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 10 2015
a) Kẻ đường cao EH của tam giác
Xét tam giác vuông DEH vuông tại H ta có
sinD = EH/ED => EH = sinD . ED = sin600 . 6 = \(\frac{\sqrt[]{3}}{2}.6=3\sqrt{3}cm\)
Diện tích tam giác DEF là : \(\frac{1}{2}\times EH\times DF=\frac{1}{2}.3\sqrt{3}.8=12\sqrt{3}\left(cm^2\right)\)
b)xét tam giác EDH có: DH = cosD . ED = 1/2 . 6 = 3 cm
ta lại có: HF = DF - DH = 8 - 3 = 5 cm
Xét tam giác vuông EHF. theo pitago ta có
EF2 = EH2 + HF = \(\left(3\sqrt{3}\right)^2+5^2=27+25=52\)
EF = \(\sqrt{52}\)
25 tháng 1 2022
Xét ΔABC có BM là đường phân giác
nên AM/AB=CM/CB
=>AM/3=CM/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{CM}{5}=\dfrac{AM+CM}{3+5}=\dfrac{4}{8}=\dfrac{1}{2}\)
Do đó: AM=1,5(cm)
Xét ΔABM vuông tại A và ΔDEF vuông tại D có
AB/DE=AM/DF
Do đó: ΔABM\(\sim\)ΔDEF
3 tháng 7 2021
\(\Delta DEF\) cho ta \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{D}=180^0-\left(\widehat{E}+\widehat{F}\right)\)
\(\Rightarrow\widehat{D}=180^0-\left(70^0+60^0\right)=180^0-130^0=50^0\)
\(Xét\) \(\Delta ABCvà\Delta DEFcó\)
\(\widehat{A}=\widehat{D}\left(=50^0\right)\)
AB=DE
AC=DF
\(\Rightarrow\Delta ABC=\Delta DEF\left(c-g-c\right)\)
Vậy \(\Delta ABC=\Delta DEF\)
J
8 tháng 4 2020
bài1
a) EF=??
b) không đồng dạng
c) không đồng dạng
d) Đồng dạng (vì sao thì bạn nhắn cho mình nha)
các cặp góc bằng nhau ABC=DEF; BCA=EFD; CAB=FDE
bài 2
a) theo tính chất đường trung bình trong mỗi tam giác (không hiểu thì nhắn cho mình)
ta có MN=1/2AB => MN/AB=1/2 (1)
NM=1/2BC => NP/BC=1/2 (2)
MP=1/2AC => MP/AC=1/2 (3)
từ (1),(2),(3) => MNP đồng dạng với ABC
b) vì MNP đồng dạng với ABC với tỉ số k là 2 ( theo câu a)
nên chu vi ABC = 2 lần chu vi MNP =40cm