cho hàm số y=-x^3+3x^2+5 có ha điểm cực trị A và B. tÍNH DIỆN TÍCH S CỦA TAM GIÁO OAB BIẾT O LÀ GỐC TỌA ĐỘ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
y = x 3 − 3 m x 2 + 4 m 3 ⇒ y ' = 3 x 2 − 6 m x . Ta có y ' = 0 ⇔ x = 0 x = 2 m
Để hàm số đã cho có 2 điểm cực trị thì m ≠ 0. Khi đó
y ' = 0 ⇔ x = 0 ⇒ y 0 = 4 m 3 ⇒ A 0 ; 4 m 3 ∈ O y x = 2 m ⇒ y 2 m = 0 ⇒ B 2 m ; 0 ∈ O x
Vậy tam giác OAB vuông tại O nên S Δ O A B = 1 2 O A . O B ⇔ 4 = 1 2 4 m 3 2 m
⇔ m 4 = 1 ⇔ m = − 1 m = 1 ⇒ S − 1 ; 1

Với mọi \(x\in R,y'=3x^2+6mx\Rightarrow y'=0\Leftrightarrow x=0\) hoặc \(x=-2m\)
Để hàm số có cực đại, cực tiểu thì phương trình \(y'=0\) có 2 nghiệm phân biệt \(\Leftrightarrow m\ne0\). Khi đó, tọa độ các điểm cực trị là \(A\left(0;2\right),B\left(-2m;4m^3+2\right)\)
\(S_{OAB}=1\Leftrightarrow OA.d\left(B;OA\right)=4\Leftrightarrow\left|2\right|=2\Leftrightarrow\begin{cases}m=1\\m=-1\end{cases}\) (thỏa mãn)
Vậy với \(m=\pm1\) thì hàm số có 2 cực trị thỏa mãn bài
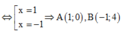
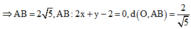

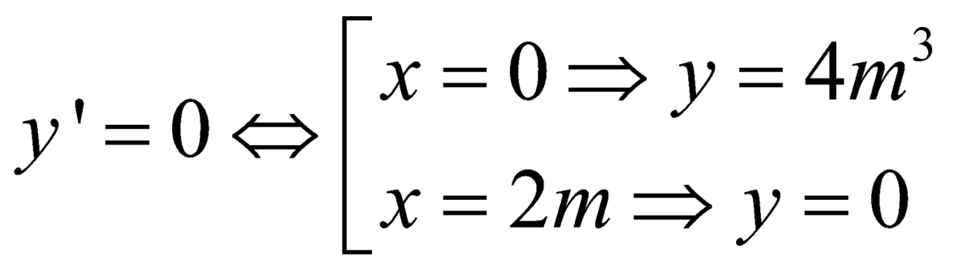
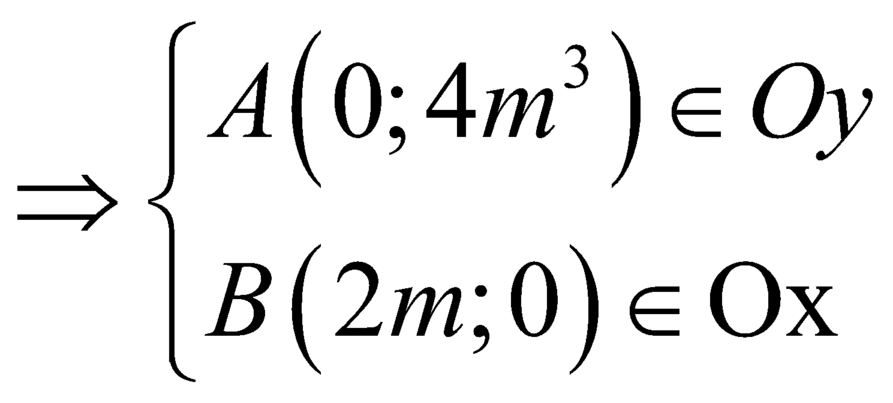
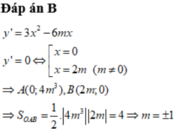
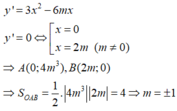

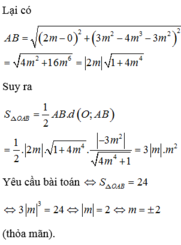
Lời giải:
Ta có: \(y=-x^3+3x^2+5\)
\(\Rightarrow y'=-3x^2+6x=0\Leftrightarrow \left[\begin{matrix} x=0\\ x=2\end{matrix}\right.\)
\(x=0\rightarrow y=5\), ta có điểm cực trị \(A=(0,5)\)
\(x=2\rightarrow y=9\), ta có điểm cực trị \(B=(2,9)\)
Do đó:
\(AB=\sqrt{(0-2)^2+(5-9)^2}=2\sqrt{5}\)
\(OA=\sqrt{0^2+5^2}=5\)
\(OB=\sqrt{2^2+9^2}=\sqrt{85}\)
Sử dụng công thức Herong: \(S=\sqrt{p(p-a)(p-b)(p-c)}\) ta suy ra
\(S_{OAB}=5\)