C94: Tập hợp các đỉnh của parabol y=x2 -2mx+2m2+3m-4 là parabol (Q). Parabol (Q) cắt trục hoành tại 2 điểm phân biệt A,B có hoành độ a,b. Tính giá trị biểu thức a2 +b2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình hoành độ giao điểm là:
\(x^2+x+1=-x^2+2x+4\)
=>\(x^2+x+1+x^2-2x-4=0\)
=>\(2x^2-x-3=0\)(1)
a=2; b=-1;c=-3
\(a\cdot c=2\cdot\left(-3\right)=-6< 0\)
=>Phương trình (1) có hai nghiệm phân biệt
Theo Vi-et, ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-1\right)}{2}=\dfrac{1}{2}\\x_1\cdot x_2=\dfrac{c}{a}=-\dfrac{3}{2}\end{matrix}\right.\)
\(P=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3\cdot x_1\cdot x_2\left(x_1+x_2\right)\)
\(=\left(\dfrac{1}{2}\right)^3-3\cdot\dfrac{-3}{2}\cdot\dfrac{1}{2}\)
\(=\dfrac{1}{8}+\dfrac{9}{4}=\dfrac{1}{8}+\dfrac{18}{8}=\dfrac{19}{8}\)

a: PTHĐGĐ là:
x^2+mx-m-2=0(1)
Khi m=2 thì (1) sẽ là
x^2+2x-2-2=0
=>x^2+2x-4=0
=>\(\left[{}\begin{matrix}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=6-2\sqrt{5}\\y=6+2\sqrt{5}\end{matrix}\right.\)
b: Δ=m^2-4(-m-2)
=m^2+4m+8
=(m+2)^2+4>0 với mọi x
=>(d) luôn cắt (P) tại hai điểm phân biệtx
x1^2+x2^2=7
=>(x1+x2)^2-2x1x2=7
=>(-m)^2-2(-m-2)=7
=>m^2+2m+4-7=0
=>m^2+2m-3=0
=>m=-3 hoặc m=1

Xét phương trình hoành độ giao điểm: x2 – 2x + m – 1 = 0
Để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương thì phương trình có hai nghiệm dương hay 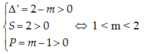
Chọn A.