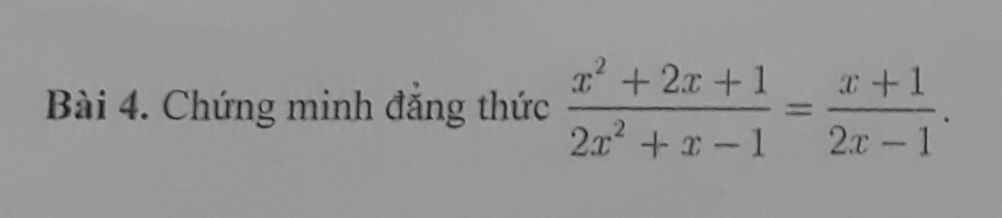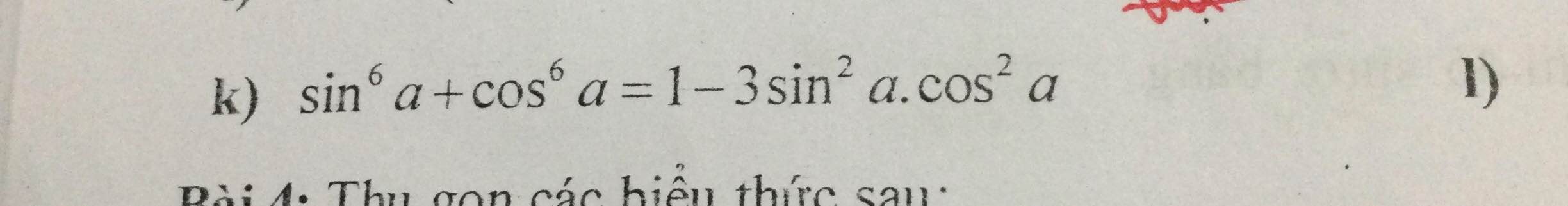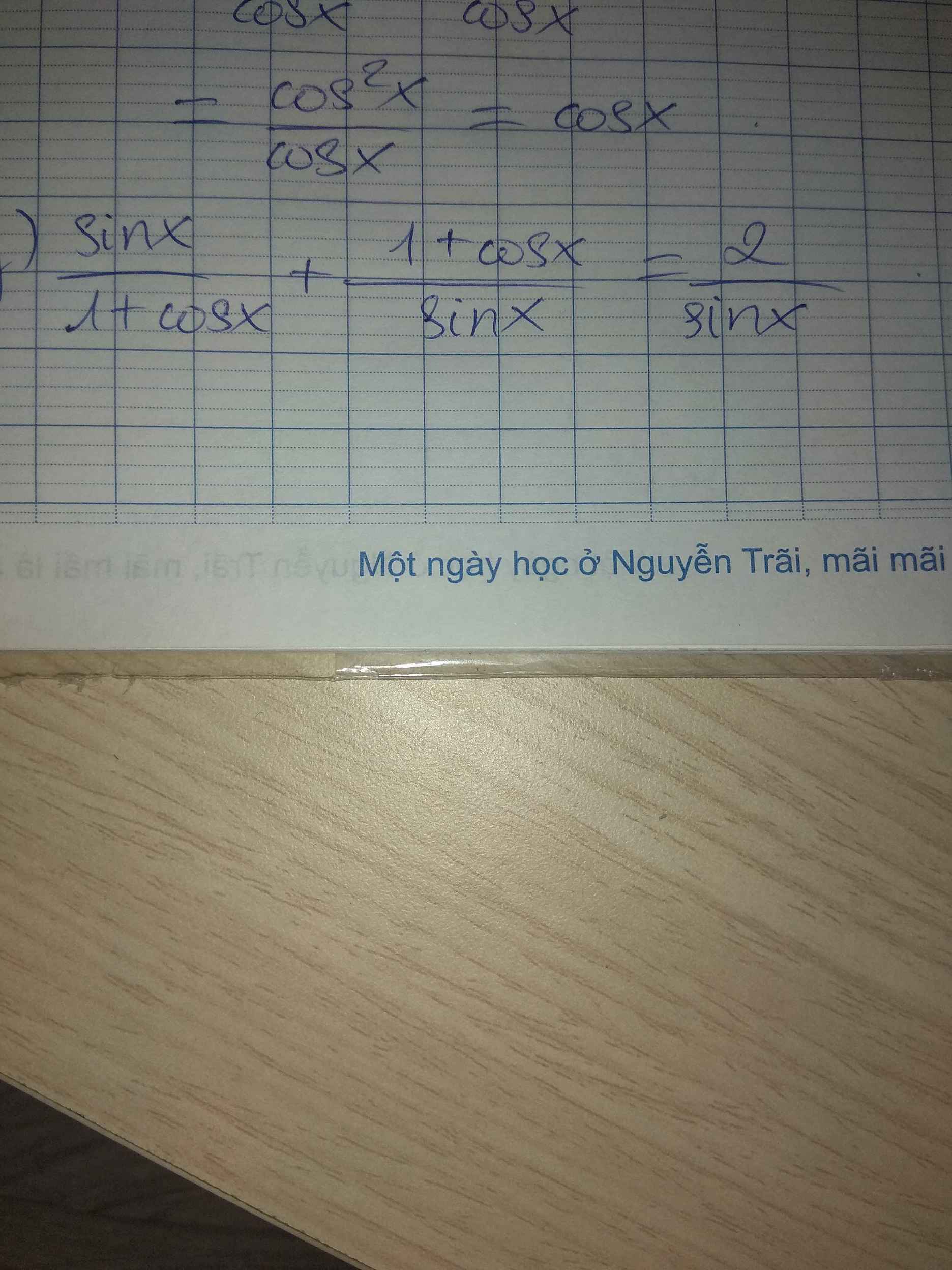chứng minh đẳng thức: 10102+10133+10152+10162=10112+10122+10142+10172
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 7 2023
\(\dfrac{x^2+2x+1}{2x^2+x-1}=\dfrac{\left(x+1\right)^2}{\left(x+1\right)\left(2x-1\right)}\)
=(x+1)/(2x-1)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 3 2022
\(sin^6a+cos^6a=\left(sin^2a\right)^3+\left(cos^2a\right)^3\)
\(=\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)\)
\(=1-3sin^2a.cos^2a\)
HP
25 tháng 3 2021
d, \(\dfrac{\left(sinx+cosx\right)^2-1}{2cotx-sin2x}=tan^2x\)
\(\Leftrightarrow\dfrac{sin^2x+cos^2x+2sinx.cosx-1}{2cotx-sin2x}=tan^2x\)
\(\Leftrightarrow2sinx.cosx=tan^2x\left(2cotx-sin2x\right)\)
\(\Leftrightarrow2sinx.cosx=\dfrac{sin^2x}{cos^2x}\left(2\dfrac{cosx}{sinx}-2sinx.cosx\right)\)
\(\Leftrightarrow sinx.cosx=\dfrac{sinx}{cosx}-\dfrac{sin^3x}{cosx}\)
\(\Leftrightarrow sinx.cos^2x=sinx-sin^3x\)
\(\Leftrightarrow sinx.cos^2x=sinx\left(1-sin^2x\right)\)
\(\Leftrightarrow sinx.cos^2x=sinx.cos^2x\)
\(\Rightarrowđpcm\)
HP
25 tháng 3 2021
a, \(\left(1-sin^2x\right).tan^2x+\left(1-cos^2x\right).cot^2x=1\)
\(\Leftrightarrow cos^2x.\dfrac{sin^2x}{cos^2x}+sin^2x.\dfrac{cos^2x}{sin^2x}=1\)
\(\Leftrightarrow sin^2x+cos^2x=1\)
\(\Rightarrowđpcm\)
b, \(1-sin^2x-sin^2x.cot^2x=0\)
\(\Leftrightarrow cos^2x-cos^2x=0\)
\(\Rightarrowđpcm\)
c, \(cos^4x+sin^2x.cos^2x+sin^2x=1\)
\(\Leftrightarrow\left(cos^2x+sin^2x\right).cos^2x+sin^2x=1\)
\(\Leftrightarrow cos^2x+sin^2x=1\)
\(\Rightarrowđpcm\)
