1 tìm x
a.92.22=(x+356):x+342
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 3 2020
a, 1/2 x 356 + 45/10 x 356 + 356 x 50/10
= 356 x ( 1/2 + 45/10 + 50/10 )
= 356 x 10
= 3560
b, x+4 + x+6 + x+8 + x+12 = 1290
(x+x+x+x) + (4+6+8+12) = 1290
4x + 30 = 1290
4x = 1290 - 30
4x = 1260
x = 1260 : 4
x = 315
12 tháng 4 2020
x+4+x+6+x+12=1290
x+ 4+6+12=1290
x+22=1290
x=1290-22
x=1268
CM
8 tháng 7 2018
a) (x + 2)2 + 3(x + 1) ≥ x2 – 4
⇔ x2 + 4x + 4 + 3x + 3 ≥ x2 – 4
⇔ 7x + 7 ≥ –4
⇔ 7x ≥ –11
⇔ x ≥ -11/7
Tập nghiệm: S = {x|x ≥ -11/7}
b)
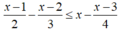
⇔ 6(x – 1) – 4(x – 2) ≤ 12x – 3(x – 3)
⇔ 6x – 6 – 4x + 8 ≤ 12x – 3x + 9
⇔ 2x + 2 ≤ 9x + 9
⇔ –7x ≤ 7 ⇔ x ≥ –1
Tập nghiệm: S = {x|x ≥ -1}
26 tháng 8 2023
\(x\left(x+1\right)=156\)
\(\Rightarrow x^2+x=156\)
\(\Rightarrow x^2+x-156=0\)
\(\Rightarrow x^2+13x-12x-156=0\)
\(\Rightarrow x\left(x+13\right)-12\left(x+13\right)=0\)
\(\Rightarrow\left(x+13\right)\left(x-12\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=12\\x=-13\end{matrix}\right.\)
___________________
\(x\left(x+1\right)=342\)
\(\Rightarrow x^2+x=342\)
\(\Rightarrow x^2+x-342=0\)
\(\Rightarrow x^2+19x-18x-342=0\)
\(\Rightarrow x\left(x+19\right)-18\left(x+19\right)=0\)
\(\Rightarrow\left(x+19\right)\left(x-18\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-19\\x=18\end{matrix}\right.\)
__________________
\(x\left(x+1\right)=650\)
\(\Rightarrow x^2+x=650\)
\(\Rightarrow x^2-x+650=0\)
\(\Rightarrow x^2+26x-25x-650=0\)
\(\Rightarrow x\left(x+26\right)-25\left(x+26\right)=0\)
\(\Rightarrow\left(x+26\right)\left(x-25\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-26\\x=25\end{matrix}\right.\)
______________________
\(x\left(x+1\right)=380\)
\(\Rightarrow x^2+x=380\)
\(\Rightarrow x^2+x-380=0\)
\(\Rightarrow x^2+20x-19x-380=0\)
\(\Rightarrow x\left(x+20\right)-19\left(x+20\right)=0\)
\(\Rightarrow\left(x+20\right)\left(x-19\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-20\\x=19\end{matrix}\right.\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 8 2023
a, \(x\).(\(x\) + 1) = 156
156 = 22.3.13 = 12.13
Vậy \(x\).(\(x\) + 1) = 12.13
Vậy \(x\) = 12
b, \(x.\)(\(x\) + 1) = 342
342 = 2.32.19 = 18.19
\(x\).(\(x+1\)) = 18.19
\(x\) = 18
c, \(x\).(\(x\) + 1) = 650
650 = 2.52.13 = 25.26
\(x\).(\(x\) +1) = 25.26
\(x\) = 25
d, \(x\).(\(x\) +1) = 380
380 = 22.5.19 = 19.20
\(x\).(\(x\) + 1) = 19.20
\(x\) = 19
2 tháng 10 2021
a) \(đk:\left\{{}\begin{matrix}x\ge0\\\sqrt{x}\ne2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
b) \(x=3+2\sqrt{2}\Rightarrow\sqrt{x}=\sqrt{3+2\sqrt{2}}=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
\(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}-2}=\dfrac{2\left(\sqrt{2}+1\right)-1}{\sqrt{2}+1-2}=\dfrac{2\sqrt{2}+1}{\sqrt{2}-1}\)
c) \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}-2}=\dfrac{1}{2}\)
\(\Leftrightarrow4\sqrt{x}-2=\sqrt{x}-2\Leftrightarrow3\sqrt{x}=0\Leftrightarrow x=0\left(tm\right)\)
d) \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}-2}>2\)
\(\Leftrightarrow2\sqrt{x}-1>2\sqrt{x}-4\Leftrightarrow-1>-4\left(đúng\forall x\right)\)
e) \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}-2}=\dfrac{2\left(\sqrt{x}-2\right)}{\sqrt{x}-2}+\dfrac{3}{\sqrt{x}-2}=2+\dfrac{3}{\sqrt{x}-2}\in Z\)
\(\Rightarrow\sqrt{x}-2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Do \(x\ge0\)
\(\Rightarrow x\in\left\{1;9;25\right\}\)
a.Ta có : 92.22=(x+356):x+342
\(\Rightarrow92.4=\left(x+356\right):x+342\)
\(\Rightarrow368=\left(x+356\right):x+342\)
\(\Rightarrow\left(x+356\right):x=26\)
\(\Rightarrow x+356=26x\)
\(\Rightarrow x+356-26x=0\)
\(\Rightarrow356-25x=0\)
\(\Rightarrow-25x=356\)
\(\Rightarrow x=-\dfrac{356}{25}\)
vậy \(x=-\dfrac{356}{25}\)