Cho nữa đường tròn tâm O , bán kính R . Trên nữa đường tròn lấy 2019 điểm A1,A2,....,A2019.
CMR:I \(\overrightarrow{OA_1}+\overrightarrow{OA_2}+...+\overrightarrow{OA_{2019}}\) I \(\ge R\)
'' I I '' là dấu giá trị tuyệt đói nhé các bạn . Các bạn giải giúp mình nhé mình đang cần

 | = |
| = | |.cos(
|.cos( ,
, 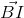 .
.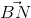 =
= 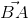 lý luận tương tự.
lý luận tương tự.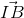 )
)