cho a,b,c≠0 CMR \(\dfrac{a^2+b^2}{b+c}+\dfrac{b^2+c^2}{c+a}+\dfrac{c^2+a^2}{a+b}\ge a+b+c\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 1 2019
3/ Áp dụng bất đẳng thức AM-GM, ta có :
\(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}\ge2\sqrt{\dfrac{\left(ab\right)^2}{\left(bc\right)^2}}=\dfrac{2a}{c}\)
\(\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge2\sqrt{\dfrac{\left(bc\right)^2}{\left(ac\right)^2}}=\dfrac{2b}{a}\)
\(\dfrac{c^2}{a^2}+\dfrac{a^2}{b^2}\ge2\sqrt{\dfrac{\left(ac\right)^2}{\left(ab\right)^2}}=\dfrac{2c}{b}\)
Cộng 3 vế của BĐT trên ta có :
\(2\left(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\right)\ge2\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)\)
\(\Leftrightarrow\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\left(\text{đpcm}\right)\)
AH
Akai Haruma
Giáo viên
4 tháng 1 2019
Bài 1:
Áp dụng BĐT AM-GM ta có:
\(\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{1}{2\sqrt{a^2.bc}}+\frac{1}{2\sqrt{b^2.ac}}+\frac{1}{2\sqrt{c^2.ab}}=\frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}{2abc}\)
Tiếp tục áp dụng BĐT AM-GM:
\(\sqrt{bc}+\sqrt{ac}+\sqrt{ab}\leq \frac{b+c}{2}+\frac{c+a}{2}+\frac{a+b}{2}=a+b+c\)
Do đó:
\(\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{2abc}\leq \frac{a+b+c}{2abc}\) (đpcm)
Dấu "=" xảy ra khi $a=b=c$
6 tháng 3 2021
Áp dụng bđt Cô-si:
\(\dfrac{a^2}{b+c}+\dfrac{b+c}{4}\ge2\sqrt{\dfrac{a^2}{b+c}\cdot\dfrac{\left(b+c\right)}{4}}=2\sqrt{\dfrac{a^2}{4}}=a\)
Chứng minh tương tự :
\(\dfrac{b^2}{c+a}+\dfrac{c+a}{4}\ge b;\dfrac{c^2}{a+b}+\dfrac{a+b}{4}\ge c\)
\(\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}+\dfrac{1}{4}\left(2a+2b+2c\right)\ge a+b+c\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge a+b+c-\dfrac{1}{2}\left(a+b+c\right)=\dfrac{a+b+c}{2}\) Dấu= xảy ra \(\Leftrightarrow a=b=c\)
KH
1
6 tháng 3 2021
Áp dụng bđt Cô-si vào các số dương a,b,c:
\(\dfrac{a^2}{b}+b\ge2\sqrt{\dfrac{a^2}{b}\cdot b}=2\sqrt{a^2}=2a\Rightarrow\dfrac{a^2}{b}\ge2a-b\)
Chứng minh tương tự ta được:
\(\dfrac{b^2}{c}\ge2b-c;\dfrac{c^2}{a}\ge2c-a\)
\(\Rightarrow\dfrac{a^2}{b}+\dfrac{b^2}{c}+\dfrac{c^2}{a}\ge2a+2b+2c-a-b-c=a+b+c\)
Dấu = xảy ra \(\Leftrightarrow a=b=c\)
PP
1
11 tháng 12 2020
Ta có: \(\dfrac{a^2}{b}+\dfrac{b^2}{c}+\dfrac{c^2}{a}\ge\dfrac{\left(a+b+c\right)^2}{a+b+c}=a+b+c\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c\)
21 tháng 9 2021
Áp dụng BĐT AG-GM:
\(\dfrac{a^3}{a^2+ab+b^2}\ge\dfrac{a^3}{a^2+\dfrac{a^2+b^2}{2}+b^2}=\dfrac{a^3}{\dfrac{3}{2}\left(a^2+b^2\right)}\)
Cmtt \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b^3}{b^2+bc+c^2}\ge\dfrac{b^3}{\dfrac{3}{2}\left(b^2+c^2\right)}\\\dfrac{c^3}{c^2+ac+a^2}\ge\dfrac{c^3}{\dfrac{3}{2}\left(c^2+a^2\right)}\end{matrix}\right.\)
Cộng vế theo vế của bất đẳng thức:
\(\Leftrightarrow VT\ge\dfrac{2}{3}\left(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+c^2}+\dfrac{c^3}{c^2+a^2}\right)\)
Tiếp tục áp dụng BĐT AG-GM:
\(\dfrac{a^3}{a^2+b^2}=\dfrac{a\left(a^2+b^2\right)-ab^2}{a^2+b^2}=a-\dfrac{ab^2}{a^2+b^2}\ge a-\dfrac{ab^2}{2ab}=a-\dfrac{b}{2}\)
Cmtt\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{b^3}{b^2+c^2}\ge b-\dfrac{c}{2}\\\dfrac{c^3}{c^2+a^2}\ge c-\dfrac{a}{2}\end{matrix}\right.\)
Cộng vế theo vế
\(\Leftrightarrow VT\ge\dfrac{2}{3}\left(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+c^2}+\dfrac{c^3}{c^2+a^2}\right)\\ \ge\dfrac{2}{3}\left(a-\dfrac{b}{2}+b-\dfrac{c}{2}+c-\dfrac{a}{2}\right)=\dfrac{2}{3}\left(a+b+c-\dfrac{a+b+c}{2}\right)=\dfrac{a+b+c}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 9 2021
\(\dfrac{a^3}{a^2+ab+b^2}=a-\dfrac{ab\left(a+b\right)}{a^2+ab+b^2}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^2.ab.b^2}}=a-\dfrac{a+b}{3}=\dfrac{2a-b}{3}\)
Tương tự và cộng lại ta sẽ có đpcm
7 tháng 3 2018
Áp dụng BĐT Cô si dạng phân số ta có :
\(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=\dfrac{a+b+c}{2}\)
=> ĐPCM .
7 tháng 3 2018
b) Vì a,b,c > 0 .
Áp dụng BĐT Cô si ta có :
\(\dfrac{a^2}{b}+b\ge2a\) (1)
Tương tự ta có : \(\dfrac{b^2}{c}+c\ge2b\) (2)
\(\dfrac{c^2}{a}+a\ge2c\) (3)
Cộng từng vế => ĐPCM .
ND
20 tháng 5 2018
Xét:
\(\dfrac{a^2}{b^2+c^2}-\dfrac{a}{b+c}=\dfrac{a\left(ab+ac-b^2-c^2\right)}{\left(b^2+c^2\right)\left(b+c\right)}=\dfrac{ab\left(a-b\right)+ac\left(a-c\right)}{\left(b^2+c^2\right)\left(b+c\right)}\left(1\right)\)
Tương tự:
\(\dfrac{b^2}{c^2+a^2}-\dfrac{b}{c+a}=\dfrac{bc\left(b-c\right)+ba\left(b-a\right)}{\left(c^2+a^2\right)\left(c+a\right)}\) (2)
\(\dfrac{c^2}{a^2+b^2}-\dfrac{c}{a+b}=\dfrac{ca\left(c-a\right)+cb\left(c-b\right)}{\left(a^2+b^2\right)\left(a+b\right)}\) (3)
Cộng từng vế (1)(2)(3) ta được:
\(\left(\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\right)-\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(=ab\left(a-b\right)\left[\dfrac{1}{\left(b^2+c^2\right)\left(b+c\right)}-\dfrac{1}{\left(a^2+c^2\right)\left(a+c\right)}\right]+ac\left(a-c\right)\left[\dfrac{1}{\left(b^2+c^2\right)\left(b+c\right)}-\dfrac{1}{\left(a^2+b^2\right)\left(a+b\right)}\right]+bc\left(b-c\right)\left[\dfrac{1}{\left(a^2+c^2\right)\left(a+c\right)}-\dfrac{1}{\left(a^2+b^2\right)\left(a+b\right)}\right]\) => ĐPCM
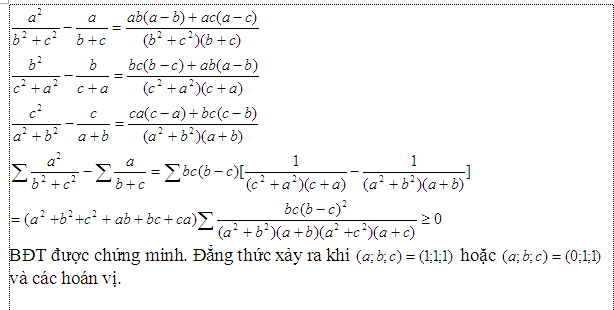
SOS helps ^^
\(\dfrac{a^2+b^2}{b+c}+\dfrac{b^2+c^2}{a+c}+\dfrac{c^2+a^2}{a+b}\ge a+b+c\)
\(\Leftrightarrow\dfrac{a^2+b^2}{b+c}-b+\dfrac{b^2+c^2}{a+c}-c+\dfrac{c^2+a^2}{a+b}-a\ge0\)
\(\Leftrightarrow\sum\dfrac{\left(a-b\right)\left(a+c\right)-\left(c-a\right)\left(a+b\right)}{b+c}\ge0\)
\(\Leftrightarrow\sum\left(a-b\right)\left(\dfrac{a+c}{b+c}-\dfrac{b+c}{a+c}\right)\ge0\)
\(\Leftrightarrow\sum\left(a-b\right)^2\dfrac{a+b+2c}{\left(a+c\right)\left(b+c\right)}\ge0\)
Cần thêm \(a;b;c\) dương nha
\(\dfrac{a^2+b^2}{b+c}+\dfrac{b^2+c^2}{c+a}+\dfrac{c^2+a^2}{a+b}\ge\dfrac{\left(a+b+b+c+c+a\right)^2}{4\left(a+b+c\right)}=a+b+c\)