Question

[Nigou Nguyễn]

1, Rút gọn các biểu thức sau :

a) ( \(\sqrt{28}\) - \(\)2\(\sqrt{3}\) + \(\sqrt{7}\) ) \(\sqrt{7}\) + \(\sqrt{84}\)

b, ( \(\sqrt{6}\) + \(\sqrt{5}\) )² - \(\sqrt{120}\)

2,Rút gọn các biểu thức sau :

a) \(\sqrt{\dfrac{a}{b}}\) + \(\sqrt{ab}\) + \(\dfrac{a}{b}\) \(\sqrt{\dfrac{b}{a}}\) với a>0 , b>0

b) \(\sqrt{\dfrac{m}{1-2x+x^2}}\) . \(\sqrt{\dfrac{4m-8mx+4mx^2}{81}}\) với m>0 và x # 1

3, Chứng minh các đẳng thức sau :

a) \(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\) \(\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2\) = 1 với a>= 0 và a #1

b) \(\dfrac{a+b}{b^2}\) \(\sqrt{\dfrac{a^2b^4}{a^2+2ab+b^2}}\) =\(\left|a\right|\) với a+b > 0 và b#0

MẤY BẠN GIỎI TOÁN GIÚP MK VỚI , THỨ 5 MK PHẢI NỘP BÀI RỒI

Answer 1

[Phùng Khánh Linh]

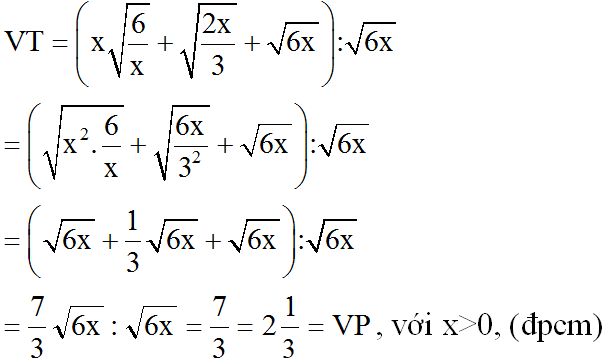
\(1a.\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}=\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}=21-2\sqrt{21}+2\sqrt{21}=21\) \(b.\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}=11+2\sqrt{30}-2\sqrt{30}=11\)

\(2a.\sqrt{\dfrac{a}{b}}+\sqrt{ab}+\dfrac{a}{b}\sqrt{\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{a}{b}.b^2}+\sqrt{\dfrac{a^2}{b^2}.\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}+b\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{a}{b}}=\left(2+b\right)\sqrt{\dfrac{a}{b}}\) \(b.\sqrt{\dfrac{m}{1-2x+x^2}}.\sqrt{\dfrac{4m-8mx+4mx^2}{81}}=\sqrt{\dfrac{m}{\left(x-1\right)^2}}.\sqrt{\dfrac{\left(2\sqrt{m}x-2\sqrt{m}\right)^2}{81}}=\dfrac{\sqrt{m}}{\text{|}x-1\text{|}}.\dfrac{\text{|}2\sqrt{m}x-2\sqrt{m}\text{|}}{9}=\dfrac{\sqrt{m}}{\text{|}x-1\text{|}}.\dfrac{2\sqrt{m}\text{|}x-1\text{|}}{9}=\dfrac{2m}{9}\) \(3a.VP=\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(\dfrac{1}{\sqrt{a}+1}\right)^2=\left(\sqrt{a}+1\right)^2.\dfrac{1}{\left(\sqrt{a}+1\right)^2}=1=VT\)

KL : Vậy đẳng thức được chứng minh.

\(b.VP=\dfrac{a+b}{b^2}.\sqrt{\dfrac{a^2b^4}{a^2+2ab+b^2}}=\dfrac{a+b}{b^2}.\dfrac{b^2\text{|}a\text{|}}{\text{|}a+b\text{|}}=\dfrac{a+b}{b^2}.\dfrac{b^2\text{|}a\text{|}}{a+b}=\text{|}a\text{|}=VT\)

KL : Vậy đẳng thức được chứng minh .

P/s : Dài v ~