Tìm m để đường thẳng y= mx cắt đồ thị hàm số \(x^3-6x^2+9x\) tại ba điểm phân biệt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 8 2021
Pt hoành độ giao điểm:
\(x^3-6x^2+9x=mx\)
\(\Leftrightarrow x\left(x^2-6x+9-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-6x+9-m=0\left(1\right)\end{matrix}\right.\)
Đường thẳng cắt đồ thị tại 3 điểm pb khi và chỉ khi (1) có 2 nghiệm pb khác 0
\(\Leftrightarrow\left\{{}\begin{matrix}9-m\ne0\\\Delta'=9-\left(9-m\right)>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>0\\m\ne9\end{matrix}\right.\)
Khi đó hoành độ A, B là nghiệm của (1) nên theo hệ thức Viet:
\(x_A+x_B=6\Rightarrow x_I=\dfrac{x_A+x_B}{2}=3\)
\(\Rightarrow\) I luôn nằm trên đường thẳng song song Oy có pt: \(x-3=0\)
CM
11 tháng 12 2018
Đồ thị hàm số y = x 2 - 9 x cắt đường thẳng y = m tại bốn điểm phân biệt khi và chỉ khi phương trình x 2 - 9 x = m (1) có bốn nghiệm phân biệt.
Đặt t = x ⇒ t 2 = x 2 phương trình (1) trở thành: t2 – 9t = m hay t2 – 9t - m= 0 (2)
Để phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi phương trình (2) có 2 nghiệm dương phân biệt:
⇔ ∆ = 81 + 4 m > 0 c a = - m > 0 - b a = 9 > 0 ⇔ m > - 81 4 m < 0 ⇔ - 81 4 < m < 0 .
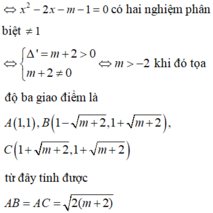
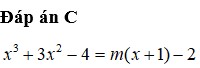
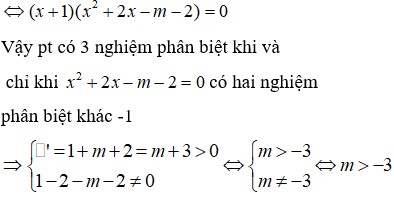
bài này chỉ cần cho mk đáp số thôi ~