Cho \(\Delta ABC\) có các đường phân giác \(\widehat{B}\) và \(\widehat{C}\) cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB và AC lần lượt tại D và E. C/minh: Hình thang BCED có một cạnh đáy bằng tổng hai cạnh bên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 9 2021
\(a,\) Các hình thang \(BDEC;BDIC;BIEC\)
\(b,DE//BC.nên.\widehat{B_1}=\widehat{I_1}\left(so.le.trong\right)\)
Mà \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right)\) nên \(\widehat{B_2}=\widehat{I_1}\Rightarrow\Delta DIB\) cân tại D
\(\Rightarrow DI=DB\left(1\right)\)
\(DE//BC.nên.\widehat{C_1}=\widehat{I_2}\left(so.le.trong\right)\)
Mà \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right)\) nên \(\widehat{C_2}=\widehat{I_2}\Rightarrow\Delta IEC\) cân tại E
\(\Rightarrow EI=EC\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI+IE=BD+EC\\ \Rightarrow DE=BD+CE\left(Đpcm\right)\)
1 tháng 10 2021
b: Xét ΔDBI có
\(\widehat{DBI}=\widehat{DIB}\)
nên ΔDBI cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=DB+EC
Vậy: BDEC là hình thang có một cạnh đáy bằng tổng hai cạnh bên
CM
22 tháng 4 2018
Đáp án cần chọn là: D
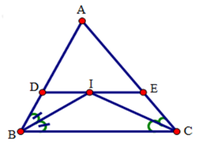
Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.
Tương tự:
Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.
Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.
CM
22 tháng 3 2017
Đáp án cần chọn là: B
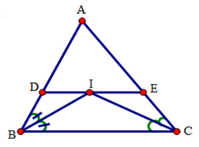
Vì DE // BC (gt) nên suy ra D I B ^ = I B C ^ (so le trong)
Mà D I B ^ = I B C ^ (gt) nên D I B ^ = D B I ^
Suy ra tam giác BDI cân đỉnh D.
Do đó DI = DB (1)
Ta có: IE // CB nên suy ra E I C ^ = B C I ^ (so le trong)
Mà E I C ^ = B C I ^ (gt) nên E C I ^ = E I C ^
Suy ra tam giác EIC cân đỉnh E
Do đó EI = EC (2)
Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE
=> DE = BD + CE
CM
26 tháng 5 2019
Đáp án cần chọn là: D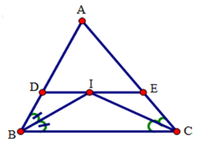
Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.
Tương tự:
Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.
Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.
CM
9 tháng 1 2018
Đáp án cần chọn là: B
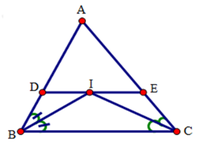
Vì DE // BC (gt) nên suy ra D I B ^ = I B C ^ (so le trong)
Mà D B I ^ = I B C ^ (gt) nên D I B ^ = D B I ^
Suy ra tam giác BDI cân đỉnh D.
Do đó DI = DB (1)
Ta có: IE // CB nên suy ra E I C ^ = B C I ^ (so le trong)
Mà B C I ^ = E C I ^ (gt) nên E C I ^ = E I C ^
Suy ra tam giác EIC cân đỉnh E
Do đó EI = EC (2)
Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE
=> DE = BD + CE
Xét ΔDIB có góc DIB=góc DBI
nên ΔDIB cân tại D
=>DI=DB
Xét ΔEIC có góc EIC=góc ECI
nên ΔEIC cân tại E
=>EI=EC
Ta có: DE=DI+IE
nên DE=DB+EC