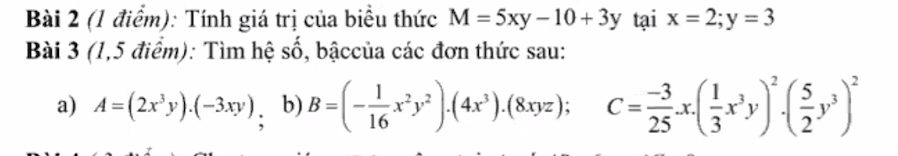Giải hộ mình bài 2 và 3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a.
\(\frac{1}{2\sqrt{2}-3\sqrt{3}}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2}-3\sqrt{3})(2\sqrt{2}+3\sqrt{3})}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2})^2-(3\sqrt{3})^2}=\frac{2\sqrt{2}+3\sqrt{3}}{-19}\)
b.
\(=\sqrt{\frac{(3-\sqrt{5})^2}{(3-\sqrt{5})(3+\sqrt{5})}}=\sqrt{\frac{(3-\sqrt{5})^2}{3^2-5}}=\sqrt{\frac{(3-\sqrt{5})^2}{4}}=\sqrt{(\frac{3-\sqrt{5}}{2})^2}=|\frac{3-\sqrt{5}}{2}|=\frac{3-\sqrt{5}}{2}\)
Bài 2.
a.
\(=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{2\sqrt{2}(\sqrt{5}+\sqrt{3})}{5-3}=\sqrt{2}(\sqrt{5}+\sqrt{3})=\sqrt{10}+\sqrt{6}\)
b.
\(=\sqrt{\frac{(2-\sqrt{3})^2}{(2-\sqrt{3})(2+\sqrt{3})}}=\sqrt{\frac{(2-\sqrt{3})^2}{2^2-3}}=\sqrt{(2-\sqrt{3})^2}=|2-\sqrt{3}|=2-\sqrt{3}\)

Câu 1:
0,9 x 218 x 2 + 0,18 x 4290 + 0,6 x 353 x 3
= 9/10 x 436 + 9/50 x 4290 + 6/10 x 1059
= 9 x 43,6 + 9 x 85,8 + 6 x 105,9
= 3 x 130,8 + 3 x 257,4 + 3 x 211,8
= 3 x ( 130,8 + 257,4 + 211,8 )
= 3 x 600
= 1800
Câu 2:
3/4 x X + 1/2 x X - 15 = 35
X x ( 3/4 + 1/2 ) - 15 = 35
X x ( 3/4 + 1/2 ) = 50
X x 5/4 = 50
X = 40
VẬy X = 40


Gọi ba số cần tìm là a,b,c
Theo đề, ta có: 2/3a=1/2b=2/5c
=>\(\dfrac{a}{1.5}=\dfrac{b}{2}=\dfrac{c}{2.5}\)
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{1.5}=\dfrac{b}{2}=\dfrac{c}{2.5}=\dfrac{a+b+c}{1.5+2+2.5}=\dfrac{240}{6}=40\)
=>a=60; b=80; c=100

22,
1, Đặt √(3-√5) = A
=> √2A=√(6-2√5)
=> √2A=√(5-2√5+1)
=> √2A=|√5 -1|
=> A=\(\dfrac{\sqrt{5}-1}{\text{√2}}\)
=> A= \(\dfrac{\sqrt{10}-\sqrt{2}}{2}\)
2, Đặt √(7+3√5) = B
=> √2B=√(14+6√5)
=> √2B=√(9+2√45+5)
=> √2B=|3+√5|
=> B= \(\dfrac{3+\sqrt{5}}{\sqrt{2}}\)
=> B= \(\dfrac{3\sqrt{2}+\sqrt{10}}{2}\)
3,
Đặt √(9+√17) - √(9-√17) -\(\sqrt{2}\)=C
=> √2C=√(18+2√17) - √(18-2√17) -\(2\)
=> √2C=√(17+2√17+1) - √(17-2√17+1) -\(2\)
=> √2C=√17+1- √17+1 -\(2\)
=> √2C=0
=> C=0
26,
|3-2x|=2\(\sqrt{5}\)
TH1: 3-2x ≥ 0 ⇔ x≤\(\dfrac{-3}{2}\)
3-2x=2\(\sqrt{5}\)
-2x=2\(\sqrt{5}\) -3
x=\(\dfrac{3-2\sqrt{5}}{2}\) (KTMĐK)
TH2: 3-2x < 0 ⇔ x>\(\dfrac{-3}{2}\)
3-2x=-2\(\sqrt{5}\)
-2x=-2√5 -3
x=\(\dfrac{3+2\sqrt{5}}{2}\) (TMĐK)
Vậy x=\(\dfrac{3+2\sqrt{5}}{2}\)
2, \(\sqrt{x^2}\)=12 ⇔ |x|=12 ⇔ x=12, -12
3, \(\sqrt{x^2-2x+1}\)=7
⇔ |x-1|=7
TH1: x-1≥0 ⇔ x≥1
x-1=7 ⇔ x=8 (TMĐK)
TH2: x-1<0 ⇔ x<1
x-1=-7 ⇔ x=-6 (TMĐK)
Vậy x=8, -6
4, \(\sqrt{\left(x-1\right)^2}\)=x+3
⇔ |x-1|=x+3
TH1: x-1≥0 ⇔ x≥1
x-1=x+3 ⇔ 0x=4 (KTM)
TH2: x-1<0 ⇔ x<1
x-1=-x-3 ⇔ 2x=-2 ⇔x=-1 (TMĐK)
Vậy x=-1

Bài 2:
Thay x=2, y=3 vào M ta có:
\(M=5xy-10+2y=5.3.2-10+3.3=30-10+9=29\)
Bài 3:
\(a,A=\left(2x^3y\right)\left(-3xy\right)=-6x^4y^2\)
Hệ số: -6
Bậc:6
\(b,B=\left(-\dfrac{1}{16}x^2y^2\right)\left(4x^3\right)\left(8xyz\right)=-2x^6y^3z\)
Hệ số: -2
Bậc:10
\(c,\dfrac{-3}{25}x\left(\dfrac{1}{3}x^3y\right)^2\left(\dfrac{5}{2}y^3\right)^2=\dfrac{-3}{25}x\left(\dfrac{1}{9}x^6y^2\right)\left(\dfrac{25}{4}y^6\right)=-\dfrac{1}{12}x^7y^8\)
Hệ số: -1/12
Bậc:15

\(\hept{\begin{cases}3^{2n}=9^n\\2^{3n}=8^n\end{cases}}\)
nếu n=0\(\Rightarrow\hept{\begin{cases}9^n=9^0=1\\8^n=8^0=1\end{cases}\Rightarrow9^n=8^n}\)
nếu n>0\(\Rightarrow9^n>8^n\)
vậy \(3^{2n}\ge2^{3n}\)