trong mp tọa độ Oxy cho Parabol (P) : y= x^2 và đt ̉ (d) : y= k(x-1) +2
1. C/M rằng với mọi k thuộc R đường thẳng (d) luôn cắt Parabol (P) tại 2 điểm phân biệt A,B
2.Giả sửA(x1;y1) ; B(x2;y2) . Tìm k thỏa mãn (x1^2 + y1) + (x2^2 + y2 ) = 14

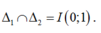
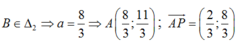
1: Phương trình hoành độ giao điểm là:
\(x^2-kx+k-2=0\)
\(\text{Δ}=\left(-k\right)^2-4\left(k-2\right)\)
\(=k^2-4k+8=\left(k-2\right)^2+4>0\)
Do đó: (P) luôn cắt (d) tại hai điểm phân biệt
2: Theo đề, ta có; \(x_1^2+x_2^2+x_1^2+x_2^2=14\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=7\)
\(\Leftrightarrow k^2-2\left(k-2\right)=7\)
\(\Leftrightarrow k^2-2k-3=0\)
=>(k-3)(k+1)=0
=>k=3 hoặc k=-1