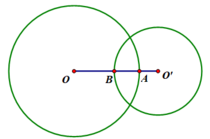
Cho (O) và (O') cắt nhau tại A và B. Kẻ cát tuyến CAD ( C trên (O), D trên (O'))
1) Chứng minh các góc của tam giác BCD không đổi khi cát tuyến quay quanh điểm A
2) Kẻ các đường kính COC', DO'D' . Chứng minh A,C', D' thẳng hàng.
3) Xác định vị trí của cát tuyến CAD sao cho đoạn thẳng CD là lớn nhất. Ở vị trí CD lớn nhất hãy chứng minh diện tích tam giác BCD bằng 4 lần diện tích tam giác OAO'
4)Biết bán kính (O) và (O') lần lượt là r và r' và góc OAO' = 90 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Sửa đề: sin x=4/5
cosx=-3/5; tan x=-4/3; cot x=-3/4
b: 270 độ<x<360 độ
=>cosx>0
=>cosx=1/2
tan x=căn 3; cot x=1/căn 3

Dễ dàng nhận thấy tam giác OAB cân tại O, và tam giác O'AC cân tại O'.
Do đó: \(\widehat{OO'C}=2\widehat{OAC};\widehat{O'OB}=180^o-2\widehat{OAB}=180^o-2\left(90^o-\widehat{OAC}\right)=2\widehat{OAC}\).
Từ đó \(\widehat{OO'C}=\widehat{O'OB}\).
Mà hai góc này ở vị trí so le trong nên OB // O'C.

a: a và (O) không có điểm chung
b: a và (O) có một điểm chung

Hình vẽ:
a, \(AH\perp MC\Rightarrow AH=HD\)
Ta có \(\left\{{}\begin{matrix}OA=OD\\HA=HD\end{matrix}\right.\Rightarrow OM\) là trung trực của \(AD\)
\(\Rightarrow MA=MD\Rightarrow\Delta OAM=\Delta ODM\left(c-c-c\right)\)
\(\Rightarrow MD\perp OD\)
Hay MD là tiếp tuyến
b, \(\Delta OAM\) vuông tại A
\(\Rightarrow O;A;M\) thuộc đường tròn đường kính OM
Lại có \(\Delta ODM\) vuông tại D
\(\Rightarrow O;D;M\) thuộc đường tròn đường kính OM
Dễ chứng minh được B là trung điểm OM
\(\Rightarrow M;A;O;D\in\left(B;R\right)\)
c, Vì \(\widehat{BAC}=90^o\Rightarrow\Delta BAC\) vuông tại A
\(\Rightarrow HB.HC=HA^2\)
Mà \(\Delta OAM\) vuông tại A \(\Rightarrow HM.HO=HA^2\)
\(\Rightarrow HB.HC=HM.HO\)

Qua phép vị tự tỉ số k biến đường tròn (O; R) thành (O’; R).
Ta có: R’ = R nên |k| = 1
Suy ra: k = 1 hoặc k = -1
* Nếu k= 1 thì phép tự là phép đồng nhất: ( mâu thuẫn giả thiết)
* Khi k=-1 thì tâm vị tự là trung điểm của OO’.
Đáp án B