tìm ghiệm của đa thức x^2-16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
DA
0
15 tháng 5 2022
Đặt \(-x^2+16=0\)
\(\Rightarrow x^2=16\)
\(\Rightarrow x=\pm\sqrt{16}\)
\(\Rightarrow x=\pm4\)
Vậy nghiệm của đa thức là \(x=\pm4\)
16 tháng 4 2017
\(x^2-15x-16=x^2+x-16x-16\)
\(=x\left(x+1\right)-16\left(x+1\right)=\left(x-16\right)\left(x+1\right)\)
làm nốt nha
NA
11 tháng 5 2017
ta có: f(x)=(x-16).(x\(^2\)+49) =0
=> \(\orbr{\orbr{\begin{cases}x-16=0\\x^2+49=0\end{cases}}}\)
=>\(\orbr{\begin{cases}x=0+16=16\\x^2=0-49=-49\end{cases}}\)
=>\(\orbr{\begin{cases}x=16\\x\in\phi\end{cases}}\)
vậy nghiệm của f(x)=16
10 tháng 8 2021
\(x^2-8x-16=x^2-2.4x+16-32=\left(x-4\right)^2-32\ge-32\)
Dấu "=" xảy ra \(\Leftrightarrow\) \(x-4=0\Leftrightarrow x=4\)
Vậy GTNN của biểu thức là -32 khi x = 4
10 tháng 8 2021
Ta có:
\(x^2-8x-16\)
⇔ ( \(x^2-2.x.4+4^2\) )\(-16\)
⇔ \(\left(x-4\right)^2-16\)
Do \(\left(x-4\right)^2\ge0\) ⇒ \(\left(x-4\right)^2-16\ge-16\)
Dấu " = " xảy ra khi x - 4 = 0 ⇔ x = 4
Vậy GTNN của A = -16 khi x = 4
NA
1
10 tháng 4 2016
\(h\left(x\right)=2x^4+x^2-16\)
Đặt t=x2
Ta được\(h\left(x\right)=2t^2+t-16\)
\(\Delta=1^2-4\cdot2\cdot\left(-16\right)=129>0=>\sqrt{\Delta}=\sqrt{129}\)
Vì \(\Delta>0\) nên đa thức h(x) có 2 nghiệm phân biệt x1,x2
\(x_1=\frac{-1+\sqrt{129}}{4}\)
\(x_2=\frac{-1-\sqrt{129}}{4}\)
PT
Cho đơn thức A = 31 / 16 x y 2 x 3 y 2 - 3 x 13 y 5 0
b. Tìm giá trị của đa thức A khi x = -1, y = 2
1
CM
11 tháng 6 2019
b. Thay x = -1, y = 2 vào A ta có: A = 31/16. (-1)7. 24 = -31 (1 điểm)
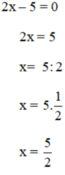
Giải:
Để đa thức \(x^2-16\) có nghiệm
Thì \(x^2-16=0\)
\(\Leftrightarrow x^2-4^2=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
Vậy ...
cho đa thức x^2-16=0
x^2 =16
x =căn 16=4