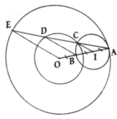
Cho đường tròn tâm O bán kính R, có hai đường kính AB và CD vuông góc với nhau.
Trên bán kính OA lấy điểm I sao cho AI=2/3 R
. Tia CI cắt đường tròn (O) tại điểm thứ hai E.
a) Chứng minh tam giác COI và tam giác CED đồng dạng
b) Tính độ dài dây CE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
12 tháng 4 2018
a, Gọi I là trung điểm của AB, ta có: OI = OA – IA
b, Ta chứng minh được IC//BD//OE
Mà OB = BI = IA => AC = CD = DE
b.
Áp dụng định lý Pitago trong tam giác vuông COI:
\(CI=\sqrt{OC^2+OI^2}=\sqrt{R^2+\left(\dfrac{R}{3}\right)^2}=\dfrac{R\sqrt{10}}{3}\)
Do 2 tam giác COI và CED đồng dạng
\(\Rightarrow\dfrac{CE}{CO}=\dfrac{CD}{CI}\Rightarrow CE=\dfrac{CD.CO}{CI}=\dfrac{2R.R}{\dfrac{R\sqrt{10}}{3}}=\dfrac{3R\sqrt{10}}{5}\)