Thanh hợp kim đồng - thiếc thứ nhất có khối lượng 10kg có tỉ lệ là 4:1 . Thanh hợp kim đồng - thiếc thứ 2 có khối lượng 16kg và có tỉ lệ 1:3 . Đem 2 thanh trên luyện thành 1 thanh hợp kim đồng-thiếc c...

1khối hợp kim A gồm thiếc và chì có khối lượng nhỏ hơn 12kg, trong đó có sẵn 5kg thiếc. Ngta cho thêm vào khối hợp kim A 15kg thiếc nữa rồi nấu chảy và thu đc 1 hỗn hợp B của thiếc và chì. Biết rằng tỉ lệ chì trong hợp kim B giảm 70% so với tỉ lệ chì trong hợp kim A. Tính khối lượng cúa khối hợp kim A.

Help me please!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

#Toán lớp 9

0

HK

hoang kim le

14 tháng 6 2019 - olm

Một chiếc chuông bằng đồng thanh ( hợp kim của đồng và thiếc ) có D = 8640 kg/m$^3$.Tính hàm lượng phần trăm của đồng trong chiếc chuông đó. Biết khối lượng riêng của đồng bằng 8,9g/cm$^3$ và khối lượng riêng của thiếc là 7,1g/cm$^3$

#Toán lớp 7

0

PT

Pham Trong Bach

12 tháng 4 2019

Một miếng hợp kim đồng và thiếc có khối lượng là 12kg, chứa 45% đồng. Hỏi phải thêm vào đó bao nhiêu thiếc nguyên chất để được hợp kim mới có chứa 40% đồng.

#Toán lớp 8

1

CM

Cao Minh Tâm

12 tháng 4 2019

Gọi x (kg) là khối lượng thiếc thêm vào. Điều kiện: x > 0.

Khối lựợng miếng hợp kim sau khi thêm là x + 12 (kg).

Khối lượng đồng có trong 12kg hợp kim chứa 45% đồng là:

12.45/100 = 5,4 (kg)

Vì khối lượng đồng không đổi trong hợp kim mới chứa 40% đồng nên ta có phương trình:

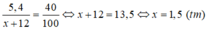
Bài 60 trang 15 SBT Toán 8 Tập 2

Vậy phải thêm vào l,5kg thiếc.

Đúng(0)

NP

Nguyễn Phương Anh

13 tháng 5 2021

Một hợp kim đồng và thiếc có khối lượng 14kg, chứa 75% đồng. Hỏi phải thêm vào đó bao nhiêu thiếc nguyên chất để được một hợp kim mới có chứa 64% đồng?

Phải thêm vào...kg thiếc nguyên chất

#Toán lớp 8

1

B

Buddy

13 tháng 5 2021

Đồng có khối lượng là:

$16 \times 64$ % $= 10, 24$ (kg)

Khối lượng hợp kim đồng và thiếc nguyên chất vào là:

$10, 24 \div 40$ % $= 25, 6$ (kg)

Khối lượng thiếc nguyên chất được thêm vào là:

$25, 6 - 10, 24 = 15, 36$ (kg)

Phải thêm vào đó $15, 36$ kg thiếc nguyên chất để được $1$ hợp kim mới chứa $40$ % đồng.

Đúng(1)

NT

Ngô Thị Quỳnh Như

15 tháng 4 2022

Để pha chế một hợp kim có khối lượng riêng là D = 5g/cm³, người ta pha trộn nhôm có khối lượng riêng 2,7g/cm³ với thiếc có khối lượng riêng 7,1g/cm³. Tính tỉ lệ phần trăm giữa nhôm và thiếc

#Vật lý lớp 8

1

NT

nguyễn thị hương giang

15 tháng 4 2022

Ta có: $D=5g$/cm³=5000kg/m³

Gọi phần trăm khối lượng của nhôm là $\%m_{Al}=a\%$

$\Rightarrow$Phần trăm khối lượng của thiếc là $\%m_{thiếc}=100\%-a\%$

Để pha chế một hợp kim:

$\Rightarrow a\%\cdot2700+\left(100\%-a\%\right)\cdot7100=5000$

$\Rightarrow a=47,73$

$\Rightarrow\dfrac{\%m_{Al}}{\%m_{thiếc}}=\dfrac{47,73\%}{100\%-47,73\%}=0,9=\dfrac{9}{10}$

Vậy $\%m_{nhôm}:\%m_{thiếc}=9:10$

Đúng(2)

SG

Sách Giáo Khoa

4 tháng 5 2017

Một miếng hợp kim đồng hồ và thiếc có khối lượng 12kg, chứa 45% đồng. Hỏi phải thêm vào đó bao nhiêu thiếc nguyên chất để được một hợp kim mới có chứa 40 % đồng ?

#Toán lớp 8

2

DN

Dương Nguyễn

4 tháng 5 2017

Trong hợp kim đồng và thiếc có khối lượng 12kg, chứa 45% đồng nên đồng có khối lượng là:

12 . 45% = 5,4 (kg)

Khối lượng hợp kim đồng và thiếc sau khi thêm thiếc nguyên chất vào (đồng vẫn giữ nguyên khối lượng) là:

5,4 : 40% = 13,5 (kg)

Khối lượng thiếc nguyên chất đã thêm vào là:

13,5 - 12 = 1,5 (kg)

Vậy phải thêm vào hợp kim đó 1,5kg thiếc nguyên chất để được một hợp kim mới có chứa 40% đồng.

Đúng(0)

NT

Nguyen Thuy Hoa

4 tháng 7 2017

Giải bài toán bằng cách lập phương trình (Tiếp).

Đúng(0)

BM

Bùi Minh Hiếu

3 tháng 4 2020 - olm

Một hợp kim đồng và thiếc có khối lượng 24kg, chứa 50% đồng. Hỏi phải thêm vào đó bao nhiêu thiếc nguyên chất để được một hợp kim mới có chứa 40% đồng?

#Toán lớp 8

1

LN

〖 Lil Nấm ⁀ᶦᵈᵒᶫᶫ〗 ²ᵏ⁶ッ

4 tháng 4 2020

Đồng có khối lượng là

24 x 50%=12(kg)

khối lượng hợp kim sau khi thêm thiếc vào là

12 : 40%=30(kg)

khối lượng thiếc nguyên chất thêm vào là

30 - 24 = 6(kg)

k cho m nha

Đúng(0)

NT

Nguyễn Thùy Mỵ Dung

16 tháng 5 2022

Một mẩu hợp kim đồng nhôm có khối lượng m = 664g, khối lượng riêng D = 8,3g/cm3. Hãy xác định khối lượng của thiếc và chì trong hợp kim. Biết khối lượng riêng của thiếc là D1= 8900kg/m3, của chì là D2 = 2700kg/m3 và coi rằng thể tích của hợp kim bằng tổng thể tích các kim loại thành phần.

#Vật lý lớp 7

1

C

☆Châuuu~~~(๑╹ω╹๑ )☆

17 tháng 5 2022

Đổi $D_1=8900kg/m^3=8,9g/m^3\\ D_2=2,7g/m^3$

Gọi lần lượt $m_1;m_2$ là khối lượng của thiếc và chì có trong hợp kim

Theo đề bài

$m_1+m_2=664\Rightarrow m_2=664-m_1$

Ta có

$V=\dfrac{m}{D}\\ \Leftrightarrow80=\dfrac{664}{8,3}\\ \Leftrightarrow80=\dfrac{m_1}{D_1}+\dfrac{m_2}{V_2}\\ \Leftrightarrow80=\dfrac{m_1}{8,9}+\dfrac{664-m_1}{2,7}$

Giải phương trình trên ta được

$\Leftrightarrow\left\{{}\begin{matrix}m_1\approx643g\\m_2=664-643\approx20,9=21g\end{matrix}\right.$

Đúng(5)

NT

Nguyễn Thùy Mỵ Dung

17 tháng 5 2022

chắc chắn đúng ko v ạ

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP