bài 1:cho hình vuông ABCD có cạnh là 1.P,Q lần lượt thuộc các cạnh AB,AD sao choPCQˆ=45độ.c/m:tam giác APQcó chu vi bằng 2.
bài2:cho hình vuôngABCD.trênAB lấy E tùy ý tia phân giác của góc CDE cắt BC tại K.c/m:AE+CK=DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
25 tháng 11 2018
Bài 1:
Do E là hình chiếu của D trên AB:
=) DE\(\perp\)AB tại E
=) \(\widehat{DE\text{A}}\)=900
Do F là hình chiếu của D trên AC:
=) DF\(\perp\)AC
=) \(\widehat{DFA}\)=900
Xét tứ giác AEDF có :
\(\widehat{D\text{E}F}\)=\(\widehat{E\text{A}F}\)=\(\widehat{DFA}\) (cùng bằng 900)
=) Tứ giác AEDF là hình chữ nhật
Xét hình chữ nhật AEDF có :
AD là tia phân giác của \(\widehat{E\text{A}F}\)
=) AEDF là hình vuông
30 tháng 12 2017
Trên tia đối tia AB lấy M sao cho AM=KC
ΔMAD = ΔKCD (c.g.c) ⇒ ˆMDA = ˆKDC⇒ˆMDK = ˆADC = 90∘
Ta có: ˆMDA+ˆAMD=90∘;ˆMDE+ˆEDK=90∘MDA^+AMD^=90∘;MDE^+EDK^=90∘
Mà ˆMDA=ˆKDC=ˆEDK⇒ˆEMD=ˆEDM⇒DE=ME=MA+EA=CK+EAMDA^=KDC^=EDK^⇒EMD^=EDM^⇒DE=ME=MA+EA=CK+EA
DD
17 tháng 4 2017
Hạ CH vuông góc PQ. Vẽ hình vuông BCEF. Trên BF lấy M sao cho PM = PQ (1)
Ta có : AP + PQ + QA = 2 = AP + PM + MF => MF = QA
=> BM = 1 - MF = 1 - QA = QD
=> tg vuông BCM = tg vuông DCQ ( vì BC = DC = 1; BM = QD) => CM = CQ (2)
Từ (1) và (2) => tg CPM = tg CPQ ( vì có CP chung; PM = PQ; CM = CQ) => ^CPH = ^CPB => tg vuông CPH = tg vuông CPB => ^PCH = ^PCB (3) và CH = CB = 1; PH = PB => QH = BM ( vì PQ = PM) => tg vuông CQH = tg vuông BMC = tg vuông DCQ => ^DCQ = ^HCQ (4)
Từ (3) và (4) => ^PCQ = ^PCH + ^HCQ = ^PCB + ^DCQ = 90o - ^PCQ => 2^PCQ = 90o => ^PCQ = 45o
24 tháng 7 2023
Bài 1:
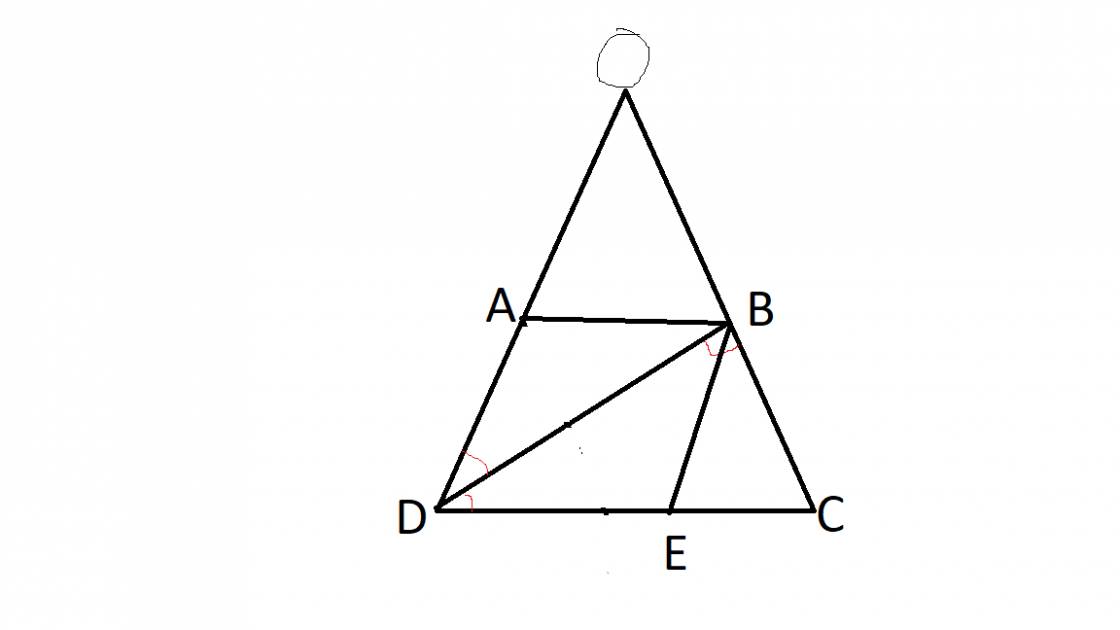
Ta có: AD=BC=3cm (t/c hthang)
Vì AB//CD(gt) nên \(\widehat{ABD}=\widehat{BDC}\left(SLT\right)\)
Mà \(\widehat{ADC}=\widehat{BDC}\) (do BD là tia pgiac góc D)
=>∠ABD=∠BDC
=>∆ABD cân tại A
=>AD=BC=3cm
Vì ∆DBC vuông tại B
nên ∠BDC+∠C=90o
Mà ∠ADC=∠C (do ABCD là hình thang cân)
và ∠BDC=1/2 ∠ADC
=> ∠BCD=1/2∠C
Khi đó: ∠C+1/2∠C=90o=>∠C=60o
- Kẻ từ B 1 đường thẳng // AD cắt CD tại E
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
Mà ∠BEC=∠ADC(đồng vị)
=>∠BEC=∠C
=>∆BEC cân tại B có ∠C=60o
=>∆BEC là ∆ cả cân cả đều
=> EC=BC=3cm
Ta có: CD = CE + ED = 3 + 3 = 6(cm)
Chu vi hình thang ABCD bằng:
AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)
24 tháng 7 2023
Bài 2:
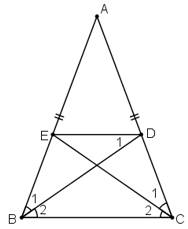
Ta có: ∆ABC là ∆ cân tại A(gt)
=>∠ABC=∠ACB
+Ta có BD là tia pgiac của ∠ABC
=>∠B1=∠B2=1/2∠ABC
+Ta có CE là tia pgiac ∠ACB
=>C1=C2=1/2∠ACB
Xét ∆
AEC và ΔADB có:
+∠A chung
+AB=AC
+C1=B1
=> ΔAEC = ΔADB
=> AE = AD
=>BCDE là hình thang cân
b) Ta có ∠ACB=∠ABC=50o(do BCDE là hình thang cân)
Ta có: ED//BC
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABC}=\widehat{AED}\\\widehat{ACB}=\widehat{ADE}\end{matrix}\right.=50^o}\) (SLT)
Mà ∠DEB=∠EDC
Ta có:
+∠DEB+∠AED=180o (kề bù)
=>50o+∠AED=180o
=>∠AED=180o-50o=130o
=>∠AED=∠ADE=130o