một học sinh thả 300g chì ở 1000C vào một cốc nước ở 25oC. Su một thời gian, nhiệt độ của chì và nước đều bằng 48oC. Tính khối lượng nước trong cốc, coi như chỉ có chì và nước truyền nhiệt cho nhau. Biết cchì = 130J/kg.K , cnước =4200J/kg.K
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 4 2023
Nhiệt lượng tỏa ra của chì:
Q1=\(m_1.c_{chì}.\left(t_1-t_{cb}\right)\)
=0,3.130.(100-48)
=2028 J
Nhiệt lượng thu vào của nước
Q2=\(m_2.c_n.\left(t_{cb}-t_2\right)\)
=4200\(m_2\).(48-25)
=4200\(m_2.23\)
=96600\(m_2\)
Theo PT cân bằng nhiệt ta có:
Q1=Q2
2028=96600\(m_2\)
=> \(m_2\)=0,02kg=20g
NV
26 tháng 4 2023
Tóm tắt:
m1 = 300g = 0,3kg
t1o = 100oC
c1 = 130J/KgK
t2o = 25oC
c2 = 4200J/KgK
to = 48oC
-------------------------------------------
Nhiệt lượng của đồng tỏa ra là:
Qtỏa = \(m_1\cdot c_1\cdot\left(t_1^o-t^o\right)\)
= \(0,3\cdot130\cdot\left(100-48\right)\)
= \(2028\) (J)
Theo PTCBN, ta có:
Qtỏa = Qthu = 2028
Qthu = \(m_2\cdot c_2\cdot\left(t^o-t_2^o\right)\)
\(2028=m_2\cdot4200\cdot\left(48-25\right)\)
\(m_2=\dfrac{2028}{4200\cdot\left(48-25\right)}=0,02\) (kg)
Vậy khối lượng của nước trong cốc là 0,02kg
#ĐN
1 tháng 7 2021
Gọi m là khối lượng nước
Có \(Q_{tỏa}=Q_{thu}\)
\(\Leftrightarrow0,2\left(100-25\right).380=m\left(25-20\right).4200\)
\(\Leftrightarrow m=\dfrac{19}{70}\left(kg\right)\)
VT
20 tháng 4 2019
Nhiệt lượng tỏa ra
Q A l = m A l . C A l ( t − 1 ) = 9900 J Q t o a = Q t h u Q H 2 O = Q t o a = 9900 J → 9900 = m H 2 O . C H 2 O ( t − t 2 ) → 9900 = m H 2 O .4200 ( 25 − 20 ) → m H 2 O = 0 , 47 k g
Đáp án: A
28 tháng 4 2023
Tóm tắt
\(m_1=300g=0,3kg\\ t_1=100^0C\\ t_2=58,5^0C\\ t=60^0C\\ \Rightarrow\Delta t_1=t_1-t=100-60=40^0C\\ \Delta t_2=t-t_2=60-58,5=1,5^0C\\ c_1=130J/kg.K\\ c_2=4200J/kg.K\)
____________________
\(m_2=?kg\)
Giải
Theo phương trình cân bằng nhiệt ta có:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\\ \Leftrightarrow0,3.130.40=m_2.4200.1,5\\ \Leftrightarrow m_2=0,25kg\)
9 tháng 5 2021
Tóm tắt:
m1 = 0,15 kg
c1 = 880 J/ kg.K
t1 = 100oC
t = 25oC
c2 = 4 200 J/ kg.K
t2 = 20oC
t = 25oC
m2 = ? kg
GIẢI:
Nhiệt lượng của quả cầu nhôm tỏa ra khi nhiệt độ hạ từ 100oC xuống 25oC là:
\(Q_1=m_1\cdot c_1\cdot\left(t_1-t\right)=0,15\cdot880\cdot\left(100-25\right)=9900\left(J\right)\)
Nhiệt lượng nước thu vào khi tăng nhiệt độ từ 20oC lên 25oC là:
\(Q_2=m_2\cdot c_2\cdot\left(t-t_1\right)=m_2\cdot4200\cdot\left(25-20\right)=m_2\cdot21000\left(J\right)\)
Nhiệt lượng cầu tỏa ra bằng nhiệt lượng nước thu vào:
\(Q_1=Q_2=9900\left(J\right)\)
\(\Rightarrow9900=m_2\cdot21000\)
\(m_2=\dfrac{9900}{21000}\simeq0,47kg\)
Z
9 tháng 5 2021
Gọi m1, c1, t1 lần lượt là khối lượng, nhiệt dung riêng và nhiệt độ ban đầu của quả cầu
m2, c2, t2 lần lượt là khối lượng, nhiệt dung riêng và nhiệt độ ban đầu của nước
Nhiệt lượng của quả cầu tỏa ra để hạ xuống 25oC là:
Qtỏa= m1.c1.(t1-25)= 0,15.880.(100-25)= 9900 J
Nhiệt lượng của nước thu vào để tăng lên 25oC là:
Qthu= m2.c2.(25-t2)= m2.4200.(25-20)= 21000m2 J
Theo PT cân bằng nhiệt, ta có: Qtỏa = Qthu
⇔ 9900= 21000m2
⇒ m2= \(\dfrac{9900}{21000}\)≃ 0,47 kg
29 tháng 7 2021
Bài này chắc là \(100^OC\) với \(60^oC\)
a, \(tc=60^oC\)
b,\(Qthu\left(nuoc\right)=\dfrac{250}{1000}.4190\left(60-58,5\right)=1571,25\left(J\right)\)
c,\(Qthu\left(nuoc\right)=Qtoa\left(chi\right)=>1571,25=\dfrac{300}{1000}.Cc.\left(100-60\right)\)
\(=>Cc=131\left(J/kgK\right)\)
H9
HT.Phong (9A5)
CTVHS
20 tháng 4 2023
Tóm tắt:
\(m_1=0,2kg\)
\(t_1=100^oC\)
\(t_2=20^oC\)
\(t=27^oC\)
\(\Rightarrow\Delta t_1=t_1-t=100-27=73^oC\)
\(\Rightarrow\Delta t_2=t-t_2=27-20=7^oC\)
\(c_1=880J/kg.K\)
\(c_2=4200J/kg.K\)
==========
\(m_2=?kg\)
Do nhiệt lượng quả cầu tỏa ra bằng nhiệt lượng của nước thu vào nên ta có phương trình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\)
\(\Leftrightarrow0,2.880.73=m_2.4200.7\)
\(\Leftrightarrow12848=29400m_2\)
\(\Leftrightarrow m_2=\dfrac{12848}{29400}\approx0,44\left(kg\right)\)
20 tháng 4 2023
Tóm tắt
\(m_1=0,2kg\)
\(t_1=100^0C\)
\(t_2=20^0C\)
\(t=27^0C\)
\(c_1=880J/kg.K\)
\(c_2=4200J/kg.K\)
________________
\(m_2=?kg\)
Giải
Theo phương trình cân bằng nhiệt ta có
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c_1.\left(t_1-t\right)=m_2.c_2.\left(t-t_2\right)\)
\(\Leftrightarrow0,2.880.\left(100-27\right)=m_2.4200.\left(27-20\right)\)
\(\Leftrightarrow12848=29400m_2\)
\(\Leftrightarrow m_2=\dfrac{12848}{29400}\)
\(\Leftrightarrow m_2=0,44kg\)
H
18 tháng 4 2023
Tóm Tắt :
\(m_1=0,15kg\)
\(C_1=880\)`J//kg.K`
\(\Delta t_1=100^oC-25^oC\)
\(C_2=4200\)`J//kg.K``
\(\Delta t_2=25^oC-20^oC\)
\(m_2=?\)
Giải
Nhiệt lượng quả cầu nhôm `0,15kg` tỏa ra để giảm nhiệt độ từ `100^o C` xuống `25^o C` là :
\(Q_{tỏa}=m_1.C_1.\Delta t_1=0,15.880\left(100-25\right)=9900\left(J\right)\)
Nhiệt lượng nước thu vào để nóng từ `20^o C` lên `25^o C` là :
\(Q_{thu}=m_2.C_2.\Delta t_2=m_2.4200.5\)
Mà \(Q_{thu}=Q_{tỏa}\) nên `2100 . m_2=9900`
`=> m_2 = 9900/21000=0,47(kg)`
H9
HT.Phong (9A5)
CTVHS
18 tháng 4 2023
Tóm tắt:
\(m_1=0,15kg\)
\(t_1=100^0C\)
\(t_2=20^oC\)
\(t=25^oC\)
\(\Rightarrow\Delta t_1=100-25=75^oC\)
\(\Rightarrow\Delta t_2=25-20=5^oC\)
\(c_1=880J/kg.K\)
\(c_2=4200J/kg.K\)
==========
\(m_2=?J\)
Do nhiệt lượng của nhôm tỏa ra bằng nhiệt lượng của nước thu vào nên ta có phương trình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\)
\(\Leftrightarrow0,15.880.75=m_2.4200.5\)
\(\Leftrightarrow m_2=\dfrac{0,15.880.75}{4200.5}\approx0,47kg\)
4 tháng 8 2021
1,\(Qtoa=0,2.880\left(100-27\right)=12848J\)
2\(Qthu=Qtoa=>12848=m.4200\left(27-20\right)=>m=0,44kg\)
4 tháng 8 2021
1.Nhiệt lượng quả cầu tỏa ra là:
Q1= m1.c1.(t1-t2)=0,2.880.(100-27)=12848 (J)
2.Khối lượng nước trong cốc là:
Ta có:Q1=Q2⇔m2.c2.(t2-t3)=Q1
⇔ \(m_2=\dfrac{Q_1}{c_2.\left(t_2-t_3\right)}=\dfrac{12848}{4200.\left(27-20\right)}=0,437\left(kg\right)\)
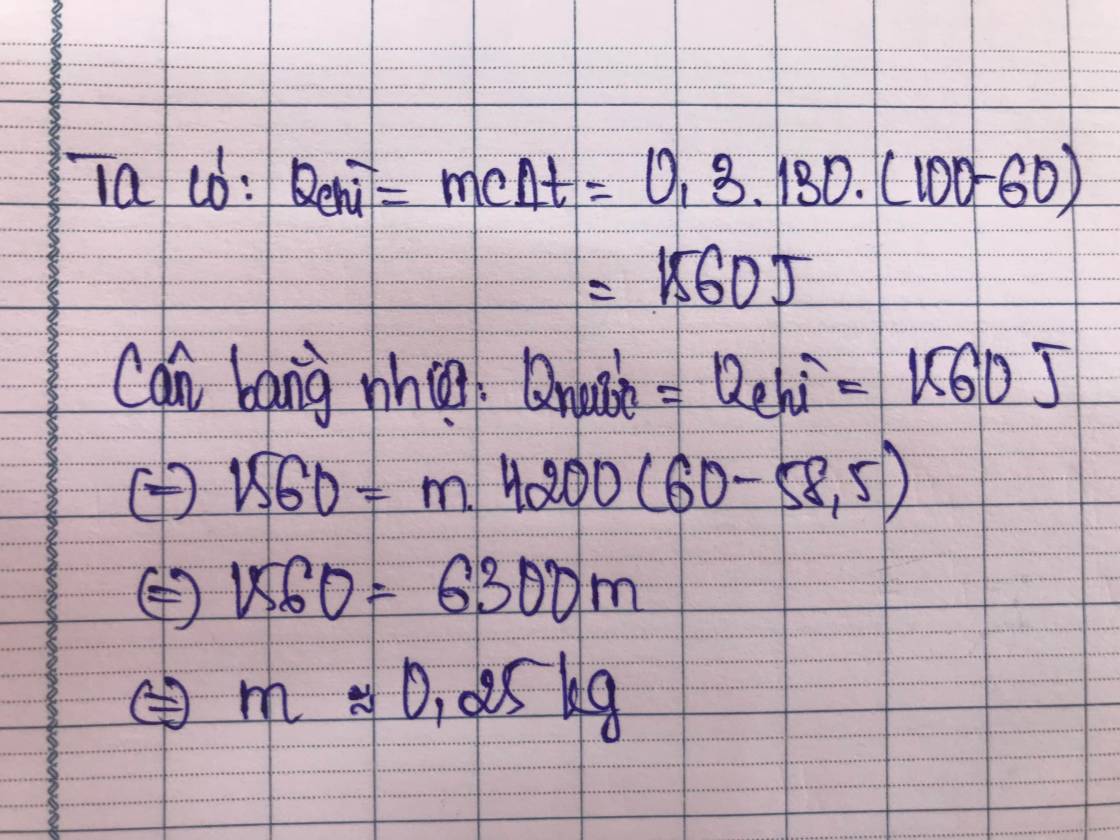
Tóm tắt:
\(m_1=300g=0,3kg\)
\(t^0_1=100^0C\)
\(c_1=130\left(J/kg.K\right)\)
\(t^0_2=25^0C\)
\(c_2=4200\left(J/kg.K\right)\)
\(t^0_c=48^0C\)
________________________
\(m_2=?\)
Giải:
Nhiệt lượng của chì tỏa ra là:
\(Q_1=m_1\Delta t^0_1c_1=m_1\left(t^0_1-t^0_c\right)c_1=0,3.\left(100-48\right)130=2028\left(J\right)\)
Nhiệt lượng của nước thu vào là:
\(Q_2=m_2\Delta t^0_2c_2=m_2\left(t^0_c-t^0_2\right)c_2=m_2\left(48-25\right)4200=96600m_2\left(J\right)\)
Theo phương trình cân bằng nhiệt, ta có:
\(Q_1=Q_2\)
\(\Leftrightarrow2028=96600m_2\)
\(\Leftrightarrow m_2=\dfrac{2028}{96600}\approx0,021\left(g\right)\)
Vậy ...