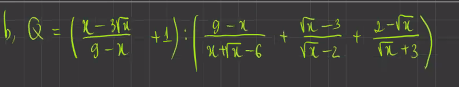
help meeee
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài sai, đề đúng phải là: \(\dfrac{1}{ab+a+1}+\dfrac{1}{bc+b+1}+\dfrac{1}{abc+ca+c}=1\)
Phản ví dụ chứng minh đề bài sai: lấy \(a=1;b=2;c=\dfrac{1}{2}\) thỏa mãn \(abc=1\)
Khi đó thay vào biểu thức:
\(\dfrac{1}{1.2+1+1}+\dfrac{1}{2.\dfrac{1}{2}+2+1}+\dfrac{1}{1.2.\dfrac{1}{2}+2.\dfrac{1}{2}+2}=\dfrac{3}{4}\ne1\)

Theo mình nghĩ thôi nhé! Bởi vì tên tập thơ như đại diện cho những kỷ niệm của chính tác giả khi còn là người lính. Như lời tác giả từng tâm sự: nhiều đêm chiến đấu, vầng trăng trên cao xuống dần và có khi như treo lơ lửng trên đầu mũi súng. Hình tượng "súng", "trăng" còn là biểu tượng cho chiến tranh và hòa bình, cái gần và xa, cái hiện thực và lãng mạn, chất chiến sĩ và chất thi sĩ,.....
Tham Khảo
“Đầu súng trăng treo” là hình ảnh rất thực và cũng rất lãng mạn:
+“Súng” và “trăng” – hai hình ảnh tưởng như đối lập song lại thống nhất hòa quyện – là cứng rắn và dịu êm – là gần và xa – là thực tại và mơ mộng – là chất chiến đấu và chất trữ tình – là chiến sĩ và thi sĩ.
+ Hiếm thấy một hình tượng nào vừa đẹp,vừa mang đầy đủ ý nghĩa như “Đầu súng trăng treo” của Chính Hữu.
+ Đây là một phát hiện, một sáng tạo bất ngờ về vẻ đẹp bình dị và cao cả trong tâm hồn người chiến sĩ. Hình tượng này góp phần nâng cao giá trị bài thơ và trở thành nhan đề cho cả tập thơ “Đầu súng trăng treo”.

Ta có: Ox//CD(gt)
\(\Rightarrow\widehat{OCD}+\widehat{COx}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{COx}=180^0-\widehat{OCD}=180^0-120^0=60^0\)
\(\Rightarrow\widehat{ACx}=\widehat{AOC}-\widehat{COx}=110^0-60^0=50^0\)
Ta có: \(\widehat{ACx}+\widehat{OAB}=50^0+130^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> AB//Cx//CD

g: =>x-1-2x+1-9+x=0
=>-9=0(vô lý)
h: \(\Leftrightarrow x^2+x-12-6x+4-x^2+8x-16=0\)
=>3x-24=0
hay x=8
i: \(\Leftrightarrow x^3+6x^2+9x-3x-x^3-6x^2-12x-8-1=0\)
=>-6x-9=0
=>6x=-9
hay x=-3/2

\(n_{Mg}=\dfrac{6}{24}=0,25\left(mol\right)\)
PTHH: \(2CH_3COOH+Mg\rightarrow\left(CH_3COO\right)_2Mg+H_2\uparrow\)
0,5<-----------0,25------->0,25------------->0,25
\(\rightarrow C_{M\left(CH_3COOH\right)}=\dfrac{0,5}{0,05}=10M\)
\(m_{dd}=100+6-0,25.2=105,5\left(g\right)\\ \rightarrow C\%_{\left(CH_3COO\right)_2Mg}=\dfrac{0,25.142}{105,5}.100\%=33,65\%\)

2. In the future, government organizations will easily access information on RFID chips.
3. I think they will introduce more effective methods of surveillance.
4. Travelling will become easier and we won't show any ID within the E.U.
5. The police will use state-of-the-art technology to improve personal security.

11 A
12 chắc hẳn thiếu remember B
13 C
14 D
15 A
16 B
17 C
18 C
19 D
20 A
21 C
22 D
ĐK: \(x\ge0;x\ne4;x\ne9\)
\(Q=\left(\dfrac{x-3\sqrt{x}}{9-x}+1\right):\left(\dfrac{9-x}{x+\sqrt{x}-6}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}+\dfrac{2-\sqrt{x}}{\sqrt{x}+3}\right)\)
\(=\left[-\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+1\right]:\left[\dfrac{9-x}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\left(2-\sqrt{x}\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right]\)
\(=\dfrac{3}{\sqrt{x}+3}:\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}.\dfrac{-\left(\sqrt{x}+3\right)}{\sqrt{x}-2}\)
\(=\dfrac{3}{2-\sqrt{x}}\)