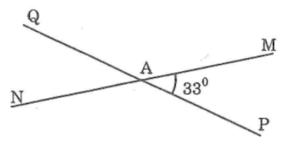
Cho hai đoạn thẳng MN và PQ cắt nhau tại điểm A. Hãy viết tên các cặp góc đối đỉnh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,có góc NAQ= goc MAP hai góc đối đỉnh
mà góc MAP =33 độ
suy ra góc NAQ=33 độ b, có gocsMAP+goc MAQ=180 hai goc ke bu goc
MAQ=180‐33=147 độ c, MAP va QAN QAM va NAP d, MAP va MAQ QAN va NAP

M N P Q A
a) Vì góc MAP và NAQ là 2 góc đối đỉnh
=> MAP = NAQ = 42o
Vì MAP và MAQ là 2 góc kề bù
=> MAP + MAQ = 180o => MAQ = 180o - 42o = 138o
b) Các cặp góc đối đỉnh: MAP và NAQ ; MAQ và NAP

a. Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = CPAM
mà ∠PAM = 33o nên ∠NAQ = 33o
b. ∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
c. Các cặp góc đối đỉnh là: ∠PAM và ∠NAQ ; ∠PAN và ∠MAQ
d. Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM
a. Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = CPAM
mà ∠PAM = 33o nên ∠NAQ = 33o
b. ∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
c. Các cặp góc đối đỉnh là: ∠PAM và ∠NAQ ; ∠PAN và ∠MAQ
d. Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM

P N A M Q 33 0
a, \(\widehat{NAQ}=\widehat{MAP}=33^0\)hai góc đối đỉnh
b, \(\widehat{MAQ}=180^0-\widehat{MAP}=180^0-33^0=147^0\)hai góc kề bù
c, Các cặp góc đối đỉnh là : \(\widehat{NAQ}\)và \(\widehat{MAP}\), \(\widehat{MAQ}\)và \(\widehat{NAP}\)
d, Các cặp góc bù nhau là : \(\widehat{MAP}\)và \(\widehat{MAQ}\), \(\widehat{MAP}\)và \(\widehat{NAP}\), \(\widehat{NAQ}\)và \(\widehat{QAM}\), \(\widehat{NAQ}\)và \(\widehat{NAP}\).

a) Ta có:
∠MAP= ∠NAQ (hai góc đối đỉnh)
⇒ ∠NAQ = 45o
⇒ ∠NAQ = 45o
b) Ta có:
∠MAP + ∠MAQ = 180o ( hai góc kề bù )
⇒ 45o + ∠MAQ = 180o
⇒ ∠MAQ = 180o − 45o = 135o
c) Các cặp góc đối đỉnh là:
∠MAP, ∠NAQ
∠NAP, ∠MAQ
d) Các cặp góc bù nhau là:
∠MAP, ∠NAP
∠MAP, ∠MAQ
∠NAQ, ∠NAP
∠NAQ, ∠MAQ