Cho tam giác ABC cân tại A có đường cao AD . Kẻ DM vuông góc với AB ( M thuộc AB ) , DN vuông góc AC tại N ( N thuộc AD ) .
a) Chứng minh AD là đường trung trực của MN .
b) Trên tia đối của DM lấy đoạn DE = DM . Chứng minh DE vuông góc CE tại E .
c) Cho biết BC = 10cm , BM = 3cm . Tính ME ?
HELP ME !!!!!!!!!!!! ~

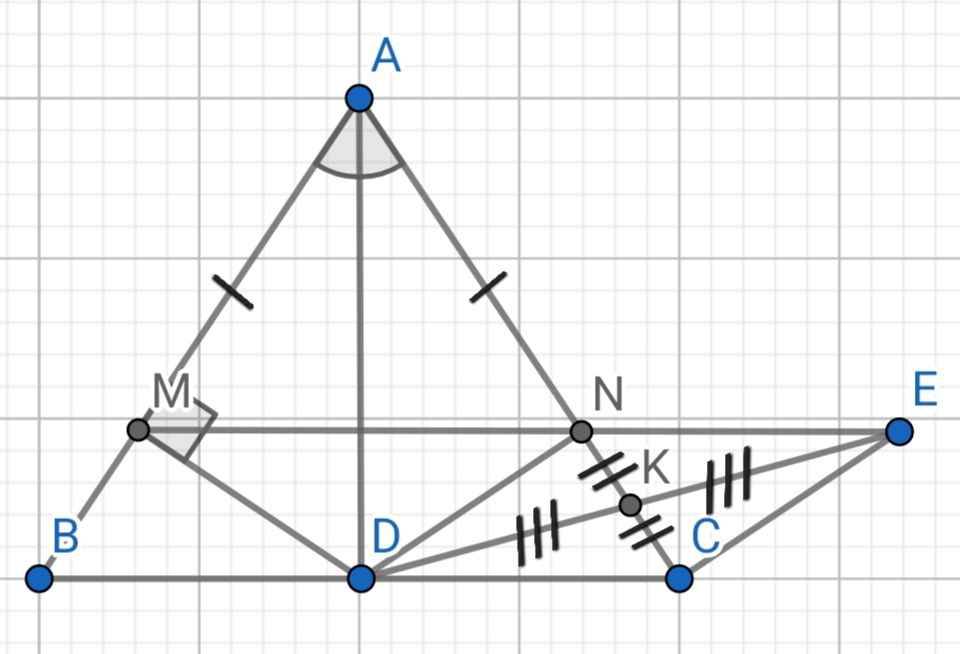
a) Xét tam giác vuông BAD và tam giác vuông ACD có
AD chung ; AB = AC
=> tam giác ABD = tam giác ACD ( ch-cgv )
=> ^BAD = ^NAD
Xét tam giác vuông AMD và tam giác vông AND có
AD chung ; ^A1 = ^A2
=> tam giác AMD = tam giác AND ( ch- gn )
=> AM = AN ; MD = ND
A và D thuộc đường trung trực của AD
=> AD là đường trung trực của MN
a) Xét tam giác ADM và tam giác ADN có :
góc AMD = góc AND ( = 90o )
AD chung
Góc DAM = góc DAN ( do tam giác ABC cân tại A)
⇒ tam giác ADM = tam giác ADN ( ch-gn)
⇒ AM = AN
⇒ tam giác AMN cân tại A
Có : AD là phân giác tại đỉnh A
⇒ AD cũng là trung trực
b) Xét tam giác DMB và tam giác DEC có :
BD = DC ( do tam giác ABC cân tại A)
Góc MDB = góc EDC ( dđ)
MD = DE (gt)
⇒ tam giác DMB = tam giác DEC (c.g.c)
⇒ DE ⊥ CE tại E
c) Ta có : BD = \(\dfrac{BC}{2}=\dfrac{10}{2}=5cm\)
Áp dụng định lý Py-ta-go vào tam giác DMB vuông tại M có:
MD2 = BD2 - BM2
MD2 = 16
MD = 4 ( MD > 0)
⇒ ME = 2.MD = 2.4 = 8cm