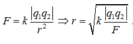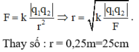. Đặt hai điện tích điểm q1 và q2 cố định lần lượt tại hai điểm A và B trong chân không thì lực đẩy giữa chúng là 10–5 N. Cố định điện tích điểm q1 và dời điện tích điểm q2 ra xa thêm một khoảng là 4...

H

Hello

12 tháng 9 2021

. Đặt hai điện tích điểm q1 và q2 cố định lần lượt tại hai điểm A và B trong chân không thì lực đẩy giữa chúng là 10–5 N. Cố định điện tích điểm q1 và dời điện tích điểm q2 ra xa thêm một khoảng là 4 mm thì lực tương tác giữa chúng khi đó là 25.10–7 N. Khoảng cách ban đầu của hai điện tích đó...

Đọc tiếp

#Vật lý lớp 11

0

HD

Hoàng Đức Long

19 tháng 5 2019

Hai điện tích điểm q 1 = 2 , 5 . 10 - 6 C và q 2 = 4 . 10 - 6 C đặt gần nhau trong chân không thì lực đẩy giữa chúng là 1,44N. Khoảng cách giữa hai điện tích là: A. 25cm B 20cm C.12cm D....

Đọc tiếp

#Vật lý lớp 11

1

VT

Vũ Thành Nam

19 tháng 5 2019

Đáp án: A

Bài tập trắc nghiệm Vật Lí 11 | Câu hỏi trắc nghiệm Vật Lí 11 có đáp án

Thay số : r = 0,25m = 25cm

Đúng(0)

HD

Hoàng Đức Long

21 tháng 1 2018

Hai điện tích điểm q 1 = 2 , 5 . 10 - 6 C và q 2 = 4 . 10 - 6 C đặt gần nhau trong chân không thì lực đẩy giữa chúng là 1,44N. Khoảng cách giữ hai điện tích là: A. 25cm B.20cm C.12cm D....

Đọc tiếp

#Vật lý lớp 11

1

VT

Vũ Thành Nam

21 tháng 1 2018

Đáp án A

Đúng(0)

VB

Vu Bao Han

24 tháng 8 2021

Cho hai điện tích điểm q1 = -10-7C và q2 = 5.10-8C đặt tại hai điểm A và B trong chân không, cách nhau một khoảng AB = 5cm.a. Xác định lực tương tác giữa hai điện tích.b. Xác định lực điện tổng hợp tác dụng lên điện tích điểm q0 = 2.10-8C đặt tại điểm C sao cho AC= 3cm, BC = 4 cm.c. Tính cường độ điện trường tại điểm...

Đọc tiếp

#Vật lý lớp 11

1

NT

Ngô Thành Chung

24 tháng 8 2021

a, Lực điện tương tác giữa hai điện tích là

Fđ = \(9.10^9.\dfrac{\left|-10^{-7}.5.10^{-8}\right|}{0.05^2}=0.018\left(N\right)\)

b, Ta có AC² + BC² = AB² (3² + 4² = 5²) nên theo định lí đảo của định lí Pitago ta có tam giác vuông ABC tại C

Lực điện tổng hợp bằng 1 nửa lực điện ở câu A (vẽ hình là thấy)

độ lớn bằng 0.009 N

c, Mình chưa học, nhưng chắc chỉ cần dùng ct là xong

Đúng(0)

HD

Hoàng Đức Long

5 tháng 6 2019

Hai điện tích điểm q 1 = 16 . 10 - 6 C v à q 2 = 4 . 10 - 6 C đặt tại hai điểm A và B trong không khí cách nhau 30 cm.a) Xác định lực tác dụng của q 1 v à q 2 b) Xác định cường độ điện trường tổng hợp do hai điện tích q 1 v à q 2 ...

Đọc tiếp

#Vật lý lớp 11

1

VT

Vũ Thành Nam

5 tháng 6 2019

a) Véc tơ lực tác dụng của điện tích q 1 l ê n q 2 có phương chiều như hình vẽ:

Có độ lớn: F 12 = k . | q 1 . q 2 | A B 2 = 9.10 9 .16.10 − 6 .4.10 − 6 0 , 3 2 = 6 , 4 ( N ) .

b) Các điện tích q 1 v à q 2 gây ra tại C các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:

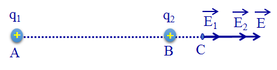
Có độ lớn: E 1 = k | q 1 | A C 2 = 9.10 9 .16.10 − 6 0 , 4 2 = 9 . 10 5 ( V / m ) ;

E 2 = k | q 2 | B C 2 = 9.10 9 .4.10 − 6 0 , 1 2 = 36 . 10 5 ( V / m ) ;

Cường độ điện trường tổng hợp tại C là:

E → = E 1 → + E 2 → có phương chiều như hình vẽ, có độ lớn:

E = E 1 + E 2 = 9 . 10 5 + 36 . 10 5 - 45 . 10 5 ( V / m ) .

c) Gọi E 1 → và E 2 → là cường độ điện trường do q 1 v à q 2 gây ra tại M thì cường độ điện trường tổng hợp do q 1 v à q 2 gây ra tại M là: E → = E 1 → + E 2 → = 0 → ð E 1 → = - E 2 → ð E 1 → và E 2 → phải cùng phương, ngược chiều và bằng nhau về độ lớn. Để thỏa mãn các điều kiện đó thì M phải nằm trên đường thẳng nối A, B; nằm trong đoạn thẳng AB (như hình vẽ).

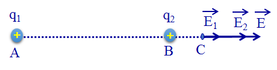
Với E 1 ' = E 2 ' ⇒ 9 . 10 9 . | q 1 | A M 2 = 9 . 10 9 . | q 2 | ( A B − A M ) 2

⇒ A M A B − A M = | q 1 | | q 2 | = 2 ⇒ A M = 2. A B 3 = 2.30 3 = 20 ( c m ) .

Vậy M nằm cách A 20 cm và cách B 10 cm.

Đúng(0)

ML

Minh Lệ

15 tháng 7 2023

Tại 3 điểm A, B, C cố định trong chân không, đặt 3 điện tích điểm có giá trị lần lượt là q₁ = 6.10^-6 C, q₂ = –6.10^-6 C và q3 = 3.10^-6 C. Biết AB = 3 cm, AC = 4 cm và BC = 5 cm. Tính độ lớn lực tác dụng lên điện tích điểm đặt tại C.

#Vật lý lớp 11

2

HQ

Hà Quang Minh

Giáo viên

5 tháng 11 2023

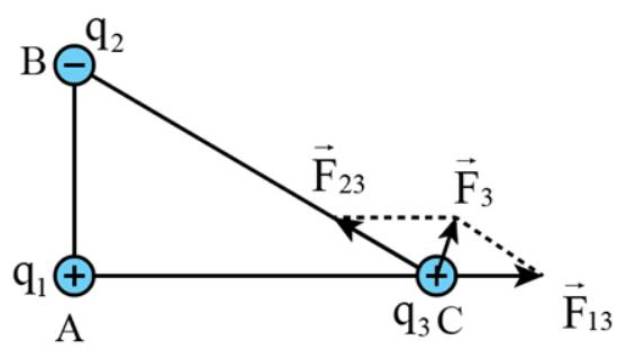
Lực tương tác giữa điện tích q₁ tác dụng lên điện tích q₃ là:

\({F_{13}} = k\frac{{\left| {{q_1}{q_2}} \right|}}{{A{C^2}}} = {9.10^9}.\frac{{\left| {{{6.10}^{ - 6}}{{.3.10}^{ - 6}}} \right|}}{{0,{{04}^2}}} = 101,25N\)

Lực tương tác giữa điện tích q₂ tác dụng lên điện tích q₃ là:

\({F_{23}} = k\frac{{\left| {{q_2}{q_3}} \right|}}{{A{C^2}}} = {9.10^9}.\frac{{\left| { - {{6.10}^{ - 6}}{{.3.10}^{ - 6}}} \right|}}{{0,{{05}^2}}} = 64,8N\)

Ta có góc tạo bởi hai vector \(\overrightarrow {{F_{13}}} \) và \(\overrightarrow {{F_{23}}} \)là α=143,13°

Độ lớn tác dụng lên điện tích q₃ là

\(F = \sqrt {F_{13}^2 + F_{23}^2 + 2{F_{13}}{F_{23}}\cos \alpha } = \sqrt {101,{{25}^2} + 64,{8^2} + 2.101,25.64,8.\cos 143,13^\circ } = 62,873N\)

Đúng(0)

HQ

Hà Quang Minh

Giáo viên

5 tháng 11 2023

Đúng(0)

HD

Hoàng Đức Long

4 tháng 10 2018

Hai điện tích q 1 = 10 - 6 C và q 2 = 4 . 10 - 6 C đặt cố định trong không khí tại hai điểm A và B cách nhau một khoảng a = 30cm. Để hệ cân bằng thì phải đặt một điện tích q 0 ở: A. trong đoạn AB, cách A l0cm B. trong đoạn AB, cách B l0cm C. ngoài đoạn AB, cách A l0cm D. ngoài đoạn AB,...

Đọc tiếp

#Mẫu giáo

1

VT

Vũ Thành Nam

4 tháng 10 2018

Đáp án A

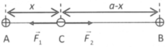
Gọi F 1 → , F 2 → là lực tĩnh điện do q 1 . q 2 tác dụng lên q 0 đặt tại C. Để q 0 nằm cân bằng thì:

F → = F 1 → + F 2 → = 0 → ⇒ F 1 → = - F 2 →

Do đó:

+ q 0 nằm trong đoạn AB (Đặt AC = x; CB = a – x)

+ hay 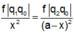(với mọi q 0 )

Hay

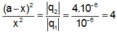
Đúng(0)

TD

Thùy Dương

9 tháng 9 2021

Hai điện tích điểm q1=2,5.10-⁶C và q2 =4.10-⁶C đặt gần nhau trong chân không thì lực đẩy giữa chúng là 1,44N.khoảng cách giữa 2 điện tích là?

#Vật lý lớp 11

1

HP

Hồng Phúc

10 tháng 9 2021

\(F=\dfrac{k.\left|q_1.q_2\right|}{r^2}\Rightarrow r=\sqrt{\dfrac{k\left|q_1.q_2\right|}{F}}=\sqrt{\dfrac{9.10^9.\left|2,5.10^{-6}.4.10^{-6}\right|}{1,44}}=0,25\left(m\right)\)

Đúng(0)

HD

Hoàng Đức Long

26 tháng 2 2018

Cho hai điện tích dương q 1 = 2 (nC) và q 2 = 0 , 018 ( μ C ) đặt cố định và cách nhau 10 (cm). Đặt thêm điện tích thứ ba q0 tại một điểm trên đường nối hai điện tích q 1 , q 2 sao cho q 0 nằm cân bằng. Vị trí của q 0 là A. c á c h q 1 2 , ...

Đọc tiếp

#Vật lý lớp 11

1