Cho hình vuông ABCD. Đường thẳng đi qua A cắt cạnh BC tại M, cắt đường thẳng DC tại N. Chứng minh rằng: 1/DC2=1/AN2+1/AM2 (vẽ thêm hình nhé)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
23 tháng 8 2023
Để chứng minh 1) AE = AN, ta sẽ sử dụng định lí hai đường trung bình của tam giác.Theo định lí hai đường trung bình, AM là đường trung bình của tam giác ABC.Vì vậy, ta có AM = 1/2(AB + AC).Đồng thời, ta cũng có AN là đường trung bình của tam giác ADC.Từ đó, ta có AN = 1/2(AD + AC).Do đó, để chứng minh AE = AN, ta cần chứng minh AE = 1/2(AB + AD).Ta biết rằng AE là đường cao của tam giác ABC với cạnh AB.Vì vậy, ta có AE = √(AB^2 - AM^2) (với AM là đường trung bình của tam giác ABC)Tương tự, ta biết rằng AN là đường cao của tam giác ADC với cạnh AD.Vì vậy, ta cũng có AN = √(AD^2 - AM^2) (với AM là đường trung bình của tam giác ADC)
30 tháng 7 2021
a) Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
\(\widehat{DEC}\) chung
Do đó: ΔBDE\(\sim\)ΔDCE(g-g)
b) Xét ΔBCD vuông tại C và ΔDHC vuông tại H có
\(\widehat{BDC}=\widehat{DCH}\)(hai góc so le trong, BD//CH)
Do đó: ΔBCD\(\sim\)ΔDHC(g-g)
Suy ra: \(\dfrac{DC}{CH}=\dfrac{BD}{CD}\)
hay \(CD^2=CH\cdot BD\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
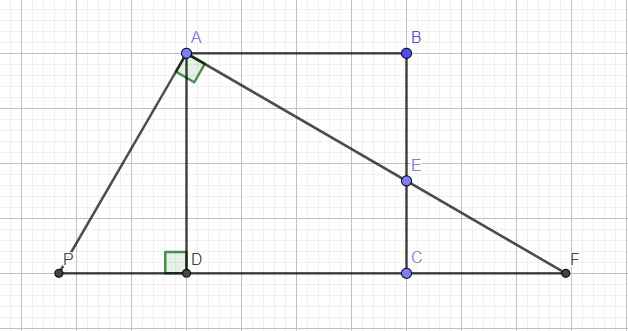
Qua A kẻ đường thẳng vuông góc AF cắt đường thẳng CD tại P
Xét hai tam giác vuông ABE và ADP có:
\(\left\{{}\begin{matrix}\widehat{B}=\widehat{D}=90^0\\AB=AD\\\widehat{BAE}=\widehat{DAP}\left(\text{ cùng phụ }\widehat{DAE}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABE=\Delta ADP\Rightarrow AP=AE\)
Áp dụng hệ thức lượng trong tam giác vuông APF:
\(\dfrac{1}{AD^2}=\dfrac{1}{AP^2}+\dfrac{1}{AF^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\) (đpcm)
Lời giải:
Do $AB\parallel CN$ nên áp dụng định lý Talet:
$\frac{AM}{MN}=\frac{AB}{CN}=\frac{DC}{CN}$
$\Rightarrow \frac{AM}{AM+MN}=\frac{DC}{DC+CN}$ hay $\frac{AM}{AN}=\frac{DC}{DN}$
$\Rightarrow AM=\frac{AN.DC}{DN}$
Do đó:
$\frac{1}{AM^2}+\frac{1}{AN^2}=\frac{DN^2}{AN^2.DC^2}+\frac{1}{AN^2}$
$=\frac{1}{AN^2}.\frac{DN^2+DC^2}{DC^2}$
$=\frac{1}{AN^2}.\frac{DN^2+AD^2}{DC^2}$
$=\frac{1}{AN^2}.\frac{AN^2}{DC^2}$ (theo định lý Pitago)
$=\frac{1}{DC^2}$
Ta có đpcm.
Hình vẽ:
