Câu 1: Cho biểu thức P=
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1 2017
Có đầy câu hỏi tương tự đáy bạn lên các câu hỏi đó mà xem
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2021
\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)
\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)
\(\Rightarrow P=4\)
\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)
\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)
\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)
A
4 tháng 2 2019
a. Ta có biến đổi:
\(A=\frac{a^3+2a^2-1}{a^3+2a^3+2a+1}\)
\(A=\frac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}\)
\(A=\frac{a^2+a-1}{a^2+a+1}\)
b. Gọi d là ước chung lớn nhất của \(a^2+a-1\)và \(a^2+a+1\)
Vì \(a^2+a-1=a\left(a+1\right)-1\)là số lẻ nên d là số lẻ
Mặt khác, \(2=\left[a^2+a+1-\left(a^2+a-1\right)\right]⋮d\)
Nên d = 1 tức là \(a^2+a+1\)và \(a^2+a-1\)nguyên tố cùng nhau.
Vậy biểu thức A là phân số tối giản.
CM
6 tháng 7 2017
Với x ≥ 0 , x ≠ 1 , x ≠ 4 ta có:
Q = x + 27 . P x + 3 x − 2 = x + 27 x + 3 = x − 9 + 36 x + 3 = x − 3 + 36 x + 3 = − 6 + x + 3 + 36 x + 3 ≥ − 6 + 12 = 6
TU
1
3 tháng 1 2024
Câu 2:
a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)
=>\(2m\ne4\)
=>\(m\ne2\)
b: Thay m=0 vào (d1), ta được:
\(y=\left(0-1\right)x+2=-x+2\)
Thay m=0 vào (d2), ta được:
\(y=\left(3-0\right)x-2=3x-2\)
Vẽ đồ thị:
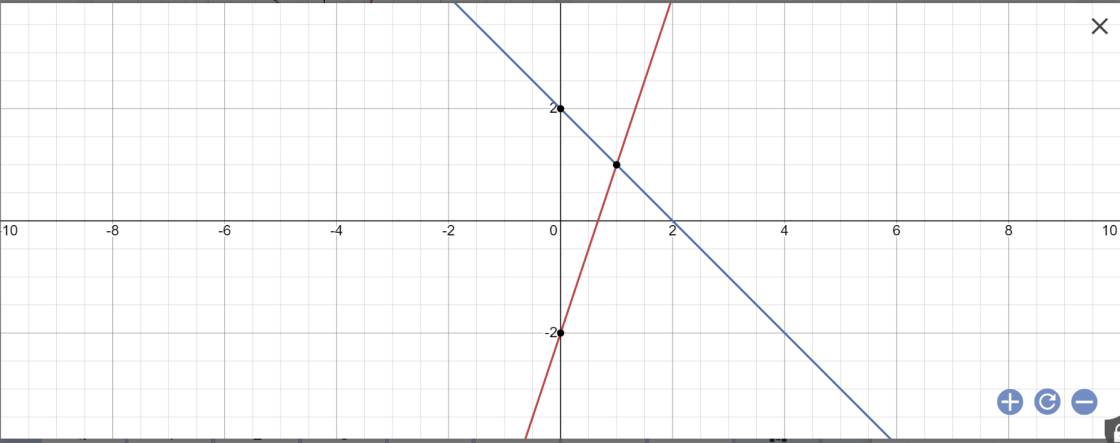
c: Phương trình hoành độ giao điểm là:
3x-2=-x+2
=>3x+x=2+2
=>4x=4
=>x=1
Thay x=1 vào y=3x-2, ta được:
y=3*1-2=3-2=1
d:
Khi m=0 thì (d2): y=3x-2
Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox
y=3x-2 nên a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq72^0\)
Câu 3:
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Ta có: AC//OM
OM\(\perp\)AB
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)CM tại E
Xét ΔMBC vuông tại B có BE là đường cao
nên \(ME\cdot MC=MB^2\)(3)
Xét ΔMBO vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)
11 tháng 11 2021
\(1,=\left(x-y\right)^2:\left(x-y\right)^2=1\\ 2,P=\left(x+y+x-y\right)^2=4x^2\\ 3,=\left(x+1\right)^2=\left(-1+1\right)^2=0\\ 4,\)
Áp dụng PTG, độ dài đường chéo là \(\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
11 tháng 11 2021
Câu 1:
\(\left(x-y\right)^2:\left(y-x\right)^2\\ =\left(x-y\right)^2:\left(x-y\right)^2\\ =1\)
Câu 2:
\(\left(x+y\right)^2+\left(x-y\right)^2+2\left(x+y\right)\left(x-y\right)=\left(x+y+x-y\right)^2=\left(2x\right)^2=4x^2\)
Câu 3:
\(x^2+2x+1=\left(x+1\right)^2=\left(-1+1\right)^2=0\)
Câu 4:
Gọi hcn đó là ABCD có chiều dài là AB, chiều rộng là AD
Áp dụng Pi-ta-go ta có:\(AB^2+AD^2=AC^2\Rightarrow AC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
Đề bài thiếu à bạn ơi!
Đề như thế này thì sao làm được.