Một người đi xe máy từ tỉnh A đến tỉnh B với vận tốc dự định là 40km/h. Sau khi đi được 1 giờ với vận tốc ấy, người đó nghĩ 15 phút và tiếp tục đi. Để đến B đúng thời gian đã định, người đó phải tăng vận tốc thêm 5 km/h. Tính quãng đường từ tỉnh A đến tỉnh B.

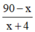 (h).
(h).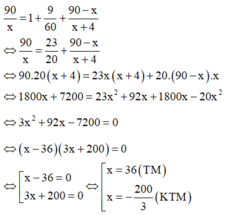
Gọi quãng đường đi từ tỉnh A đến tỉnh B là: a (km, a>0)
Thời gian đi từ tỉnh A đến tỉnh B theo dự định là: \(\dfrac{a}{40}\) (h)
Thời gian đi từ tỉnh A đến B sau 1h là: \(\dfrac{a-40}{45}\) (h)
Theo bài ra, ta có phương trình:
\(\dfrac{a}{40}=1+\dfrac{1}{4}+\dfrac{a-40}{45}\)
<=>\(\dfrac{9a}{360}=\dfrac{360}{360}+\dfrac{90}{360}+\dfrac{8\left(a-40\right)}{360}\)
<=> \(9a=360+90+8a-320\)
<=> \(a=130\)
Vậy quãng đường đi từ tỉnh A đến tỉnh B dài 130 km.