Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài làm:
a, \(\Delta AHF\&\Delta CHD\)Có:
\(\widehat{AHF}=\widehat{CHD}\left(đv\right),\widehat{AFH}=\widehat{CDH}=90^o\)
\(\Rightarrow\Delta AHF\infty\Delta CHD\left(g.g\right)\)
\(\Rightarrow\frac{HA}{HC}=\frac{HF}{HD}\Rightarrow HA.HD=HC.HF\)
b, Sửa N thành B
\(\Delta BAD\&\Delta BCF\)Có:
\(\widehat{B}chung,\widehat{D}=\widehat{F}=90^o\)
\(\Rightarrow\Delta BAD\infty\Delta BCF\left(g.g\right)\)
\(\Rightarrow\frac{BA}{BC}=\frac{BD}{BF}\Rightarrow BF.BA=BD.BC\)
c,Vì \(\frac{BA}{BC}=\frac{BD}{BF}\Rightarrow\frac{BD}{BA}=\frac{BF}{BC}\)
\(\Delta BFD\&\Delta BCA\)Có:
\(\widehat{B}chung,\frac{BF}{BC}=\frac{BD}{BA}\)
\(\Rightarrow\)\(\Delta BFD\infty\Delta BCA\left(c.g.c\right)\)
\(\Rightarrow\widehat{BFD}=\widehat{BCA}\)
d, chưa nghĩ ra
Câu hỏi của Ngọc Duyên DJ - Toán lớp 8 - Học toán với OnlineMath
câu trả lời đã được đăng cách đây 2 ngày nhé
Hình bạn tự vẽ nha
a, Xét \(\Delta AHF\) và \(\Delta CHD\) có
\(\widehat{HFA}\)=\(\widehat{HDC}\)=\(90^o\)
\(\widehat{AHF}=\widehat{CHD}\)(đối đỉnh)
\(\Rightarrow\Delta AHF\infty\Delta CHD\)( g-g)
\(\Rightarrow\frac{AH}{CH}=\frac{HF}{HD}\)\(\Rightarrow AH\cdot HD=CH\cdot HF\)
a, Xét tam giác BAD và tam giác CAE có
^A _ chung
^BDA = ^CEA = 900
Vậy tam giác BAD ~ tam giác CAE (g.g)
b, => ^ABD = ^ACE (2 góc tương ứng)
Xét tam giác HBE và tam giác HCD ta có
^HBE = ^HCE (cmt)
^BHE = ^CHD (đ.đ)
Vậy tam giác HBE ~ tam giác HCD (g.g)
\(\dfrac{HB}{HC}=\dfrac{HE}{HD}\Rightarrow HD.HB=HE.HC\)
c, xem lại cách viết cạnh tương ứng tam giác bạn nhé
Xét tam giác BHC và tam giác EHD ta có
\(\dfrac{BH}{EH}=\dfrac{HC}{HD}\)(tỉ lệ thức của tỉ số đồng dạng trên)
^BHC = ^EHD (đ.đ)
Vậy tam giác BHC ~ tam giác EHD (c.g.c)
hình bạn tự vẽ nha
a, Xét \(\Delta AHF\)và \(\Delta CHD\)có
\(\widehat{AHF}=\widehat{CHD}\)(đối đỉnh)
\(\widehat{AFH}=\widehat{CDH}=90^o\)
\(\Rightarrow\Delta AHF\infty\Delta CHD\left(g\cdot g\right)\)\(\Rightarrow\frac{AH}{CH}=\frac{HF}{HD}\)\(\Rightarrow HA\cdot HD=HC\cdot HF\)
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
Do đo: ΔABD đồng dạg với ΔACE
Suy ra: AD/AE=AB/AC
hay \(AD\cdot AC=AB\cdot AE\) và AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
Do đo: ΔADE đồng dạng với ΔABC
Suy ra: góc ADE=góc ABC
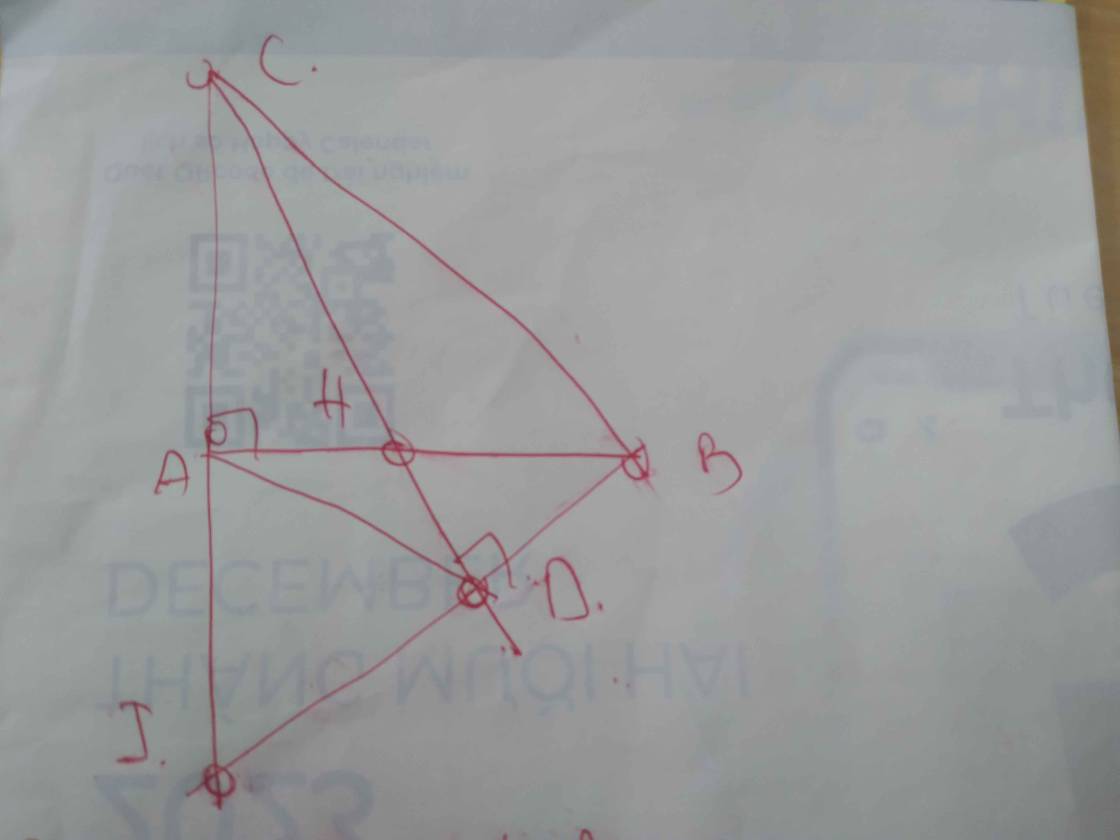
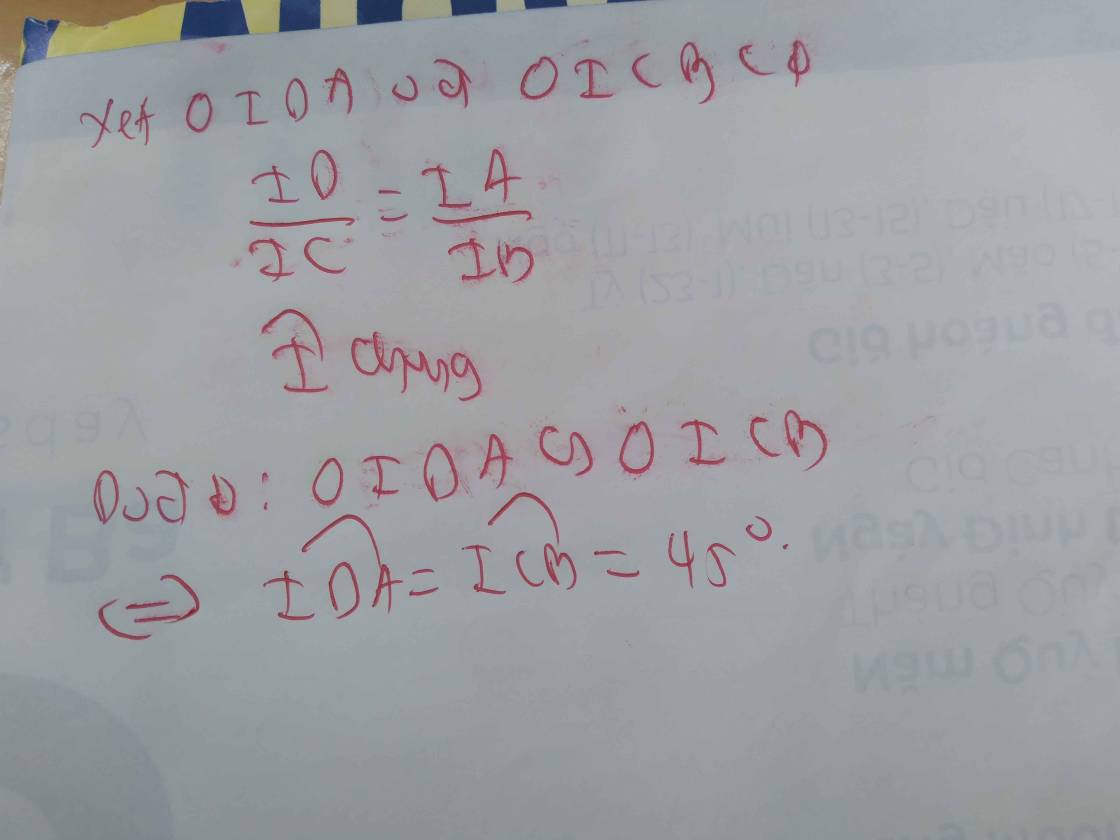
a: Xét ΔAHF vuông tại F và ΔCHD vuông tại D có
góc AHF=góc CHD
Do đó: ΔAHF đồng dạng với ΔCHD
b: Xét ΔBFC vuông tại F và ΔBDA vuông tại D có
góc B chung
Do đó: ΔBFC đồng dạng với ΔBDA
Suy ra: BF/BD=BC/BA
hay \(BF\cdot BA=BC\cdot BD\) và BF/BC=BD/BA
c: Xét ΔBFD và ΔBCA có
BF/BC=BD/BA
góc FBD chung
Do đó:ΔBFD đồng dạng với ΔBCA