cho abc lần lượt là độ dài 3 cạch của tam giác abc. chứng minh rằng tanA/tanB=
a2+c2-b2/b2+c2-a2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
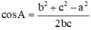
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.

Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)

Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:
Δ = (b2 + c2 - a2)2 - 4b2c2
= (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
= [(b - c)2 - a2][(b + c)2 - a2]
= (b – c – a)(b – c + a)(b + c + a)(b + c – a).
Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:
b < c + a ⇒ b – c – a < 0
c < a + b ⇒ b – c + a > 0
a < b + c ⇒ b + c – a > 0
a, b, c > 0 ⇒ a + b + c > 0
⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).

1.
Sửa đề: \(S=\dfrac{1}{6}\left(ch_a+bh_c+ah_b\right)\)
\(a.h_a=b.h_b=c.h_c=2S\Rightarrow\left\{{}\begin{matrix}h_a=\dfrac{2S}{a}\\h_b=\dfrac{2S}{b}\\h_c=\dfrac{2S}{c}\end{matrix}\right.\)
\(\Rightarrow6S=\dfrac{2Sc}{a}+\dfrac{2Sb}{c}+\dfrac{2Sa}{b}\)
\(\Leftrightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}=3\)
Mặt khác theo AM-GM: \(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\ge3\sqrt[3]{\dfrac{abc}{abc}}=3\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c\)
\(\Leftrightarrow\) Tam giác đã cho đều
2.
Bạn coi lại đề, biểu thức câu này rất kì quặc (2 vế không đồng bậc)
Ở vế trái là \(2\left(a^2+b^2+c^2\right)\) hay \(2\left(a^3+b^3+c^3\right)\) nhỉ?
3.
Theo câu a, ta có:
\(VT=\dfrac{2S}{a}+\dfrac{2S}{b}+\dfrac{2S}{c}\ge\dfrac{18S}{a+b+c}=\dfrac{18.pr}{a+b+c}=9r\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c\)
Hay tam giác đã cho đều

a) Vì a, b, c là độ dài 3 cạnh của một tam giác
⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
⇒ a + c – b > 0 và a + b – c > 0
Ta có: (b – c)2 < a2
⇔ a2 – (b – c)2 > 0
⇔ (a – (b – c))(a + (b – c)) > 0
⇔ (a – b + c).(a + b – c) > 0 (Luôn đúng vì a + c – b > 0 và a + b – c > 0).
Vậy ta có (b – c)2 < a2 (1) (đpcm)
b) Chứng minh tương tự phần a) ta có :
( a – b)2 < c2 (2)
(c – a)2 < b2 (3)
Cộng ba bất đẳng thức (1), (2), (3) ta có:
(b – c)2 + (c – a)2 + (a – b)2 < a2 + b2 + c2
⇒ b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2 < a2 + b2 + c2
⇒ 2(a2 + b2 + c2) – 2(ab + bc + ca) < a2 + b2 + c2
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).
\(\dfrac{\tan A}{\tan B}=\dfrac{\sin A}{\cos A}.\dfrac{\cos B}{\sin B}=\dfrac{\dfrac{a.\sin B}{b}\left(\dfrac{a^2+c^2-b^2}{2ac}\right)}{\dfrac{b^2+c^2-a^2}{2bc}.\sin B}=\dfrac{\dfrac{\sin B.\left(a^2+c^2-b^2\right)}{2bc}}{\dfrac{\sin B.\left(b^2+c^2-a^2\right)}{2bc}}=\dfrac{a^2+c^2-b^2}{b^2+c^2-a^2}\)