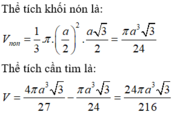hãy nêu cách vẽ hình tam giác và đường tròn nội tiếp của tam giác bằng phần mềm geogebra
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2023
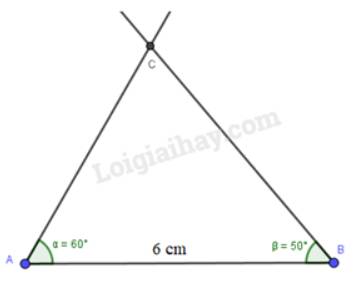
a) Xét tam giác ABC, áp dụng định lí tổng 3 góc trong tam giác, ta có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \\ \Rightarrow \widehat {ABC} = 180^\circ - (\widehat {BAC} + \widehat {ACB}) = 180^\circ - (60^\circ + 70^\circ ) = 50^\circ \end{array}\)
Bước 1: Vẽ AB = 6 cm
Bước 2: Vẽ \(\widehat {BAB'} = 60^\circ \)bằng cách:
Chọn công cụ Góc, nháy chuột lần lượt vào các điểm B, A ( theo chiều ngược kim đồng hồ) nhập số đo góc 60
Bước 3: Vẽ \(\widehat {ABA'} = 50^\circ \) bằng cách:
Chọn công cụ Góc, nháy chuột lần lượt vào các điểm A,B ( theo chiều kim đồng hồ) nhập số đo góc 50
Bước 4: Vẽ điểm C là giao điểm của AB’ và BA’
b)
Nháy chuột vào Hồ sơ. Chọn xuất bản. Chọn hiển thị đồ thị dạng hình rồi lưu ảnh dạng png
18 tháng 9 2023
a) Bước 1: Vẽ đoạn thẳng AB = 4 cm
Bước 2: Vẽ đường thẳng qua A và vuông góc với AB bằng cách
Chọn công cụ Đường vuông góc, chọn đường vuông góc, nháy chuột vào điểm A và đoạn AB
Bước 3: Vẽ đoạn AC = 3 cm
Bước 4: Vẽ đoạn thẳng BC
Nháy chuột vào Hồ sơ. Chọn xuất bản. Chọn hiển thị đồ thị dạng hình rồi lưu ảnh dạng png
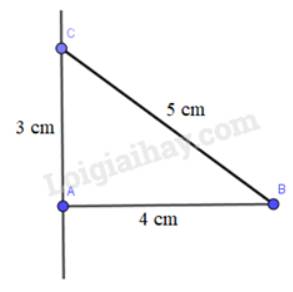
b) Bên trái màn hình hiển thị độ dài đoạn thẳng BC = 5 cm
PT
Thế nào là đường tròn nội tiếp một tam giác? Nêu cách xác định tâm của đường tròn nội tiếp tam giác.
1
CM
11 tháng 2 2017
- Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác.
- Tâm đường tròn nội tiếp tam giác là giao điểm của các tia phân giác của các góc trong của tam giác.
CM
22 tháng 6 2019
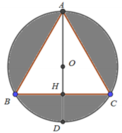
Đáp án C
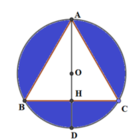
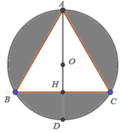
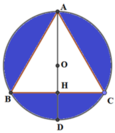
Phương pháp: Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng thể tích hình cầu đường kính AD trừ đi thể tích hình nón tạo bởi khi quay tam giác ABC quanh trục AD.
Cách giải:
*) Tính thể tích hình cầu đường kính AD:
Tam giác ABC đều, cạnh a
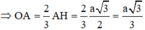
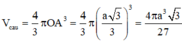
*) Tính thể tích hình nón (H) tạo bởi khi quay tam giác ABC quanh trục AH:
Hình nón (H) có đường cao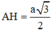 
, bán kính đáy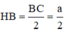 
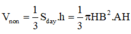
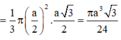
*) Tính V
CM
18 tháng 11 2019
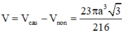
Thể tích cần tìm bằng thể tích của khối cầu đường kính AD trừ đi thể tích khối nón sinh bởi tam giác ABC khi quay quanh trục AD.
+) ∆ A D C vuông tại C ⇒ a D = A C c o s D A C = a 3 2 = 2 a 3
⇒ Bán kính khối cầu đường kính AD là: R = a 3
⇒ V c a u = 4 3 π . a 3 3 = 4 πa 3 3 27
+) ∆ A B C đều cạnh a ⇒ A H = a 3 3 r = H B = H C = a 2
Thể tích khối nón là:
V n o n = 1 3 π ( a 2 ) 2 . a 3 2 = πa 3 3 24
Thể tích cần tìm là:
V = 4 πa 3 3 27 - πa 3 3 24 = 24 πa 3 3 216
Chọn đáp án D.