Chứng minh chu kì tuần hoàn của y=tan x là \(\pi\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Đây là tính chất của hàm y = tan x . có tan x + π = tan x ∀ x ∈ D

a. TXĐ: \(D=R\)
Với mọi \(x\in D\Rightarrow x\pm2\pi\in D\)
Đồng thời:
\(y\left(x+2\pi\right)=sin\left(x+2\pi\right)+cos\left(2x+4\pi\right)=sinx+cos2x=y\left(x\right)\)
\(\Rightarrow\) Hàm là hàm tuần hoàn với chu kì \(T=2\pi\)
b. TXĐ: \(D=R\)
Với mọi \(x\in D\Rightarrow x\pm\dfrac{2\pi}{3}\in D\)
\(y\left(x+\dfrac{2\pi}{3}\right)=sin\left(3x+2\pi\right)=sin3x=y\left(x\right)\)
\(\Rightarrow\) Hàm là hàm tuần hoàn với chu kì \(T=\dfrac{2\pi}{3}\)

Hàm số y=3*sin2x tuần hoàn theo chu kì là:
\(T=\dfrac{2\Omega}{2}=\Omega\)
=>Chọn C

Đáp án B
Hướng dẫn Theo đầu bài hai nguyên tố kế tiếp nhau nên cách nhau một điện tích dương. Giả sử ZX, ZY là số proton của X và Y
![]()
Cấu hình electron của X 1s22s22p63s2 ,X ở chu kì 3 nhóm IIA
Cấu hình electron của Y 1s22s22p63s23p1 ,Y ở chu kì 3 nhóm IIIA
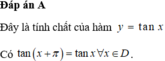

TXĐ: \(D=R\backslash\left\{\dfrac{\pi}{2}+k\pi\right\}\)
\(\forall x\in D\Rightarrow x+\pi\in D\) và \(x-\pi\in D\)
\(f\left(x+\pi\right)=tan\left(x+\pi\right)=tanx=f\left(x\right)\)
\(\Rightarrow\) Hàm y=tanx tuần hoàn với chu kì \(\pi\)