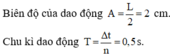Giúp e vs. Một vật dao động điều hòa trên đoạn thẳng dài 8cm và thực hiện được 12 dao động toàn phần trong 3s. Tìm biên độ, tần số, chu kì, tần số góc của dao động.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=\(\frac{10}{2}\) =5
T=\(\frac{10}{50}\) =0.2 s
ω=\(\frac{2\pi}{T}\) =\(\frac{2\pi}{O.2}\) =10π (rad/s)
f=\(\frac{1}{T}\) =\(\frac{1}{0.2}\) =5 (Hz) \
Tại vị trí cân bằng : v=ωA=10π*5=50π
a=ω2 *A=(10π)2 *5 =50.102 (cm/s2 )
Cái này mk vẫn đag thắc mắc gia tốc có đi qua vị trí cân bằng hay ko nên nếu ko đi qua thì bạn lm như sau nhé : x=\(\sqrt{A^2-\frac{v^2}{\omega^2}}\) =\(\sqrt{25-\frac{2500}{1000}}\) =\(\frac{3\sqrt{10}}{2}\)
→a=-ω2 *A=-1000*\(\frac{3\sqrt{10}}{2}\)=-4743 (cm/s)

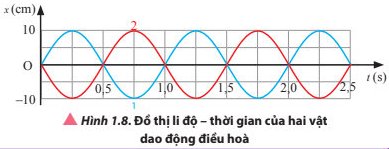
Hai dao động có cùng biên độ.
Ở cùng một thời điểm khi dao động 1 ở vị trí cân bằng thì dao động 2 ở vị trí bên và ngược lại.

Biên độ: A=3
Tần số góc: pi
Chu kì: T=2pi/pi=2
Pha dao động: pi*t
Pha ban đầu: 2pi

a. Biên độ của dao động là: \(A=10\) (cm)
Tần số góc là: \(\omega=2\pi\) (rad/s)
Tần số là: \(f=\dfrac{\omega}{2\pi}=1\) (Hz)
Chu kì là: \(T=\dfrac{1}{f}=1\) (s)
b. Vận tốc và gia tốc cực đại lần lượt là:
\(v_{max}=\omega A=20\pi\) (cm/s)
\(a_{max}=\omega^2A=400\) (cm/s)
c. Phương trình vận tốc là:
\(v=20\pi\cos\left(2\pi t+\dfrac{\pi}{2}\right)\) (cm/s)