Trong mặt phẳng oxy cho tam giác abc có đỉnh A thuộc d: x-2y-1=0 và cạnh BC song song với d. đường cao BH: x-y-2=0. Trung điểm cạnh AC là M(1;3). Tìm tọa độ các đỉnh A,B,C của tam giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
AC vuông góc BH nên nhận (1;-1) là 1 vtpt
Phương trình AC:
\(1\left(x-1\right)-1\left(y-1\right)=0\Leftrightarrow x-y=0\)
A thuộc AC và d nên tọa độ A là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x-4y-2=0\end{matrix}\right.\) \(\Rightarrow A\left(-\dfrac{2}{3};-\dfrac{2}{3}\right)\)
M là trung điểm AC \(\Rightarrow\left\{{}\begin{matrix}x_C=2x_M-x_A=\dfrac{8}{3}\\y_C=2y_M-y_A=\dfrac{8}{3}\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{8}{3};\dfrac{8}{3}\right)\)
BC song song d nên nhận (1;-4) là 1 vtpt
Phương trình BC:
\(1\left(x-\dfrac{8}{3}\right)-4\left(y-\dfrac{8}{3}\right)=0\Leftrightarrow x-4y+8=0\)
B là giao điểm của BC và BH nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x-4y+8=0\\x+y+3=0\end{matrix}\right.\) \(\Rightarrow B\left(-4;1\right)\)
\(\Rightarrow\overrightarrow{AB}=...\Rightarrow\) phương trình đường thẳng AB
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\x-2y-2=0\end{matrix}\right.\) \(\Rightarrow B\left(0;-1\right)\)
Gọi vtpt của đường thẳng CM (cũng là đường cao kẻ từ C) có tọa độ \(\left(a;b\right)\)
H là chân đường cao kẻ từ B
\(cos\widehat{HBC}=\dfrac{\left|1.1+1.\left(-2\right)\right|}{\sqrt{1^2+1^2}.\sqrt{1^2+\left(-2\right)^2}}=\dfrac{1}{\sqrt{10}}\)
\(\Rightarrow cos\widehat{MCB}=cos\widehat{HBC}=\dfrac{1}{\sqrt{10}}=\dfrac{\left|a+b\right|}{\sqrt{a^2+b^2}.\sqrt{1^2+1^2}}\)
\(\Leftrightarrow\sqrt{a^2+b^2}=\sqrt{5}\left|a+b\right|\Leftrightarrow a^2+b^2=5\left(a+b\right)^2\)
\(\Leftrightarrow2a^2+5ab+2b^2=0\Leftrightarrow\left(a+2b\right)\left(2a+b\right)=0\)
Chọn \(\left(a;b\right)=\left[{}\begin{matrix}\left(2;-1\right)\\\left(1;-2\right)\end{matrix}\right.\) (trường hợp (1;-2) loại do song song BH)
\(\Rightarrow\) Phương trình đường cao kẻ từ C:
\(2\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow2x-y-3=0\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\2x-y-3=0\end{matrix}\right.\) \(\Rightarrow C\left(...\right)\)
Gọi N là trung điểm BC \(\Rightarrow\) tọa độ N
Tam giác ABC cân tại A \(\Rightarrow\) AN là trung tuyến đồng thời là đường cao
\(\Rightarrow\) Đường thẳng AN vuông góc BC \(\Rightarrow\) nhận (1;-1) là 1 vtpt và đi qua N
\(\Rightarrow\) Phương trình AN
Đường thẳng AB vuông góc CM nên nhận (1;2) là 1 vtpt
\(\Rightarrow\) Phương trình AB (đi qua B và biết vtpt)
\(\Rightarrow\) Tọa độ A là giao điểm AB và AN
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
Hướng dẫn, hơi dài nên làm biếng giải chi tiết:
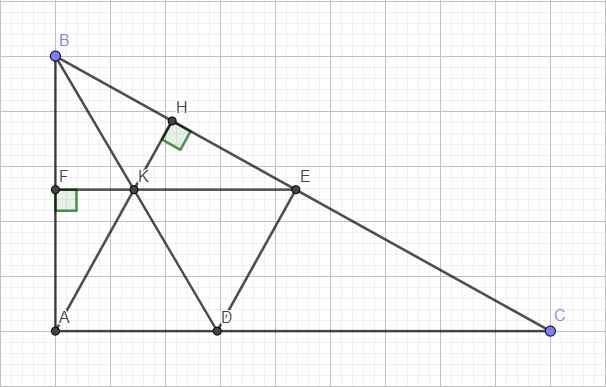
Kéo dài KE cắt AB tại F
BK là phân giác góc B nên hai tam giác vuông BKH và BKF bằng nhau (ch-gn)
\(\Rightarrow\widehat{BKF}=\widehat{BKE}\) \(\Rightarrow\widehat{BKA}=\widehat{BKE}\)
\(\Rightarrow\Delta BKA=\Delta BKE\left(g.c.g\right)\)
\(\Rightarrow AK=EK\)
Lại có \(\widehat{BKF}=\widehat{BDA}\) (đồng vị) \(\Rightarrow\widehat{BDA}=\widehat{BKH}=\widehat{AKD}\)
\(\Rightarrow\Delta AKD\) cân tại A hay \(AK=AD\)
\(\Rightarrow AD=EK\Rightarrow ADEK\) là hình bình hành hay DE song song AK (hay AH)
BC vuông góc AH nên nhận (3;1) là 1 vtpt và đi qua E(3;-7) \(\Rightarrow\) pt BC
ED đi qua E(3;-7) và song song AH nên nhận (1;-3) là 1 vtpt \(\Rightarrow\) pt DE
\(\Rightarrow\) Tọa độ D (giao của DE và \(\Delta\))
ADEK là hbh (theo cmt) và có 2 cạnh kề AK=AD nên ADEK là hình thoi
\(\Rightarrow AD=DE\)
Biết tọa độ D, E \(\Rightarrow\) độ dài DE
A thuộc AH nên tọa độ A có dạng: \(A\left(3a+16;a\right)\Rightarrow\overrightarrow{DA}=...\Rightarrow\left|\overrightarrow{DA}\right|=DE\)
\(\Rightarrow a\Rightarrow\) tọa độ A
\(\Rightarrow\) Phương trình AC (qua A và D)
\(\Rightarrow\) Phương trình AB (qua A và vuông góc AC)
NM
Nguyễn Minh Quang
Giáo viên
31 tháng 3 2022
ta có tọa độ B là nghiệm của hệ \(\hept{\begin{cases}x-2=0\\2x+3y=1\end{cases}\Leftrightarrow B\left(2;-1\right)}\)
Từ I kẻ d' qua I và song song với BC khi đó \(d':x=-7\)
Khi đó d' cắt AC tại điểm K có tọa độ là \(\hept{\begin{cases}x=-7\\2x+3y=1\end{cases}\Leftrightarrow}K\left(-7;5\right)\), gọi H là trung điểm của BC
khi đó điểm A thuộc trung trực của KI là đường thẳng AH: \(y=1\)Do đó tọa độ A là : \(A\left(-1;1\right)\)
Do đó đường cao từ C có VTPT \(IA=\left(6,4\right)\)nên đường cao từ C là : \(3x+2y-4=0\)