Cíu cíu !!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 was repaired
2 Was - bought
3 are watered
4 wasn't learned
5 was watched
6 Is - read
7 was stolen
8 was broken
9 wasn't cut
10 is cleaned

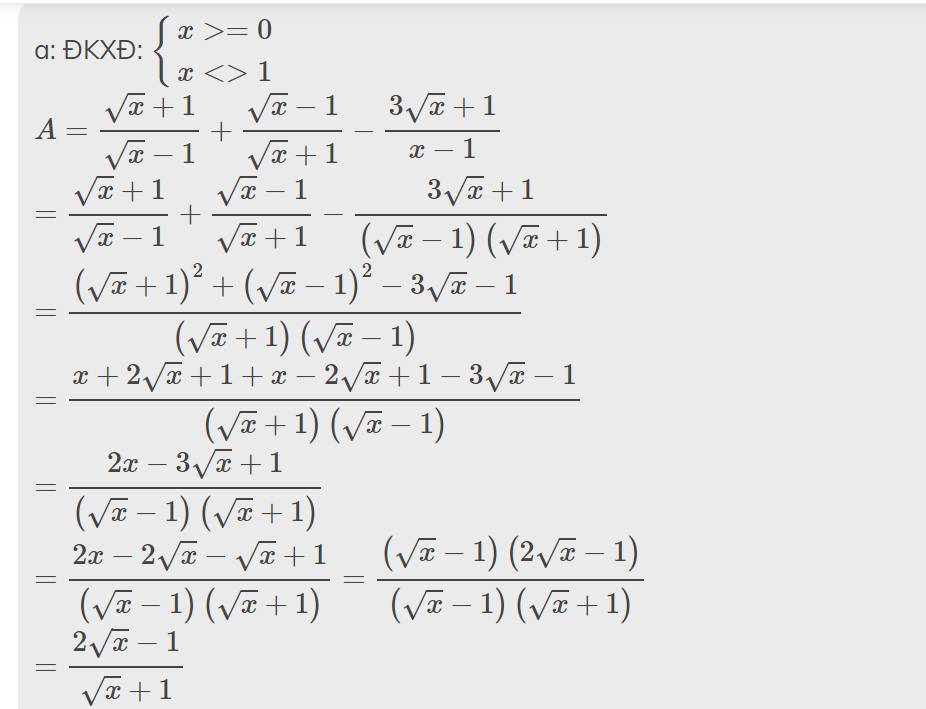
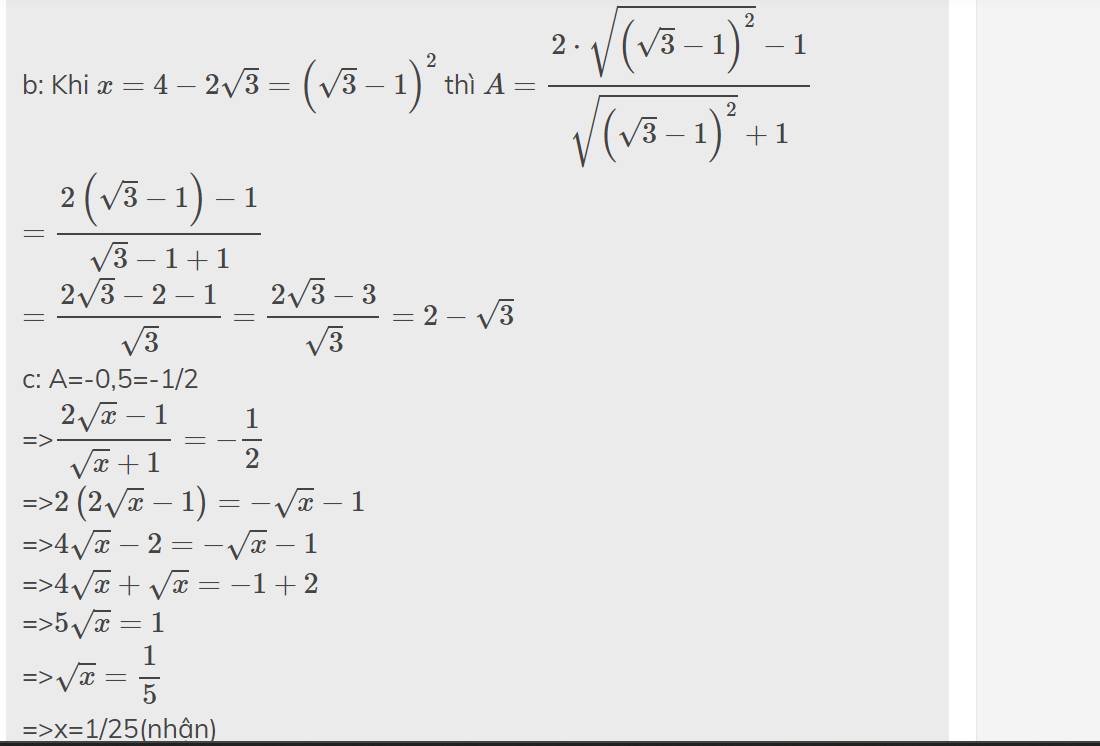

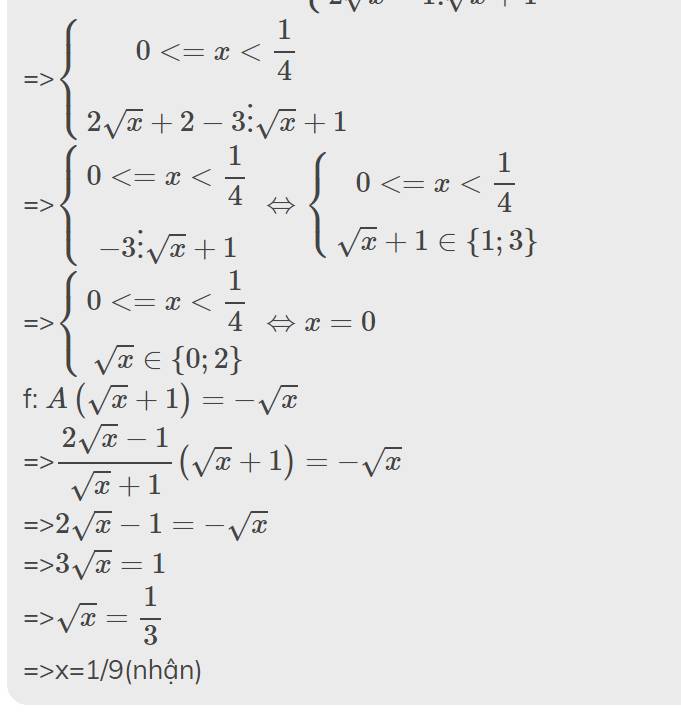
g: A<1
=>\(\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}< 1\)
=>\(\dfrac{2\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}+1}< 0\)
=>\(\sqrt{x}-2< 0\)
=>\(\sqrt{x}< 2\)
=>0<=x<4
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< =x< 4\\x< >1\end{matrix}\right.\)
h: \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
=>\(A=\dfrac{2\sqrt{x}+2-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\)
\(\sqrt{x}+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(\dfrac{3}{\sqrt{x}+1}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{3}{\sqrt{x}+1}>=-3\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{3}{\sqrt{x}+1}+2>=-3+2=-1\forall x\) thỏa mãn ĐKXĐ
=>\(A>=-1\forall x\) thỏa mãn ĐKXĐ
Vậy: \(A_{min}=-1\) khi x=0
i: \(P=A\left(-x+2\sqrt{x}+3\right)\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\cdot\left(-1\right)\cdot\left(x-2\sqrt{x}-3\right)\)
\(=\dfrac{1-2\sqrt{x}}{\sqrt{x}+1}\cdot\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)\)
\(=\left(1-2\sqrt{x}\right)\left(\sqrt{x}-3\right)\)
\(=\sqrt{x}-3-2x+6\sqrt{x}=-2x+7\sqrt{x}-3\)
\(=-2\left(x-\dfrac{7}{2}\sqrt{x}+\dfrac{3}{2}\right)\)
\(=-2\left(x-2\cdot\sqrt{x}\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{1}{16}\right)\)
\(=-2\left(\sqrt{x}-\dfrac{7}{4}\right)^2+\dfrac{1}{8}< =\dfrac{1}{8}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}-\dfrac{7}{4}=0\)
=>\(\sqrt{x}=\dfrac{7}{4}\)
=>\(x=\dfrac{49}{16}\)


1: Xét ΔMNP vuông tại M có MH là đường cao
nên MH^2=HN*HP; MN^2=NH*NP; PM^2=PH*PN
=>MH=căn 3,6*6,4=4,8cm; MN=căn 3,6*10=6cm; PM=căn 6,4*10=8cm
2: MK=8/2=4cm
Xét ΔMNK vuông tại M có tan MNK=MK/MN=4/6=2/3
nên \(\widehat{MNK}\simeq33^041'\)
3: ΔMNK vuông tại M có MF là đường cao
nên NF*NK=NM^2
ΔMNP vuông tại M có MH là đường cao
nên NH*NP=NM^2
=>NF*NK=NH*NP


a) \(\sqrt[]{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
\(\Leftrightarrow\sqrt[]{3\left(x^2+2x+1\right)+4}+\sqrt{5\left(x^2+2x+1\right)+9}=-\left(x^2+2x+1\right)+5\)
\(\Leftrightarrow\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}=-\left(x+1\right)^2+5\left(1\right)\)
Ta có :
\(\left\{{}\begin{matrix}\sqrt[]{3\left(x+1\right)^2+4}\ge2,\forall x\in R\\\sqrt[]{5\left(x+1\right)^2+9}\ge3,\forall x\in R\end{matrix}\right.\)
\(\Rightarrow VT=\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}\ge5,\forall x\in R\)
\(VP=-\left(x+1\right)^2+5\le5,\forall x\in R\)
Dấu "=" xảy ra thì \(VT=VP=5\)
\(\left(1\right)\Leftrightarrow\left(x+1\right)^2=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy nghiệm của phương trình đã cho là \(x=-1\)

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot9=36\)
=>\(AH=\sqrt{36}=6\left(cm\right)\)
b: Xét (O) có
ΔAEH nội tiếp
AH là đường kính
Do đó; ΔAEH vuông tại E
=>HE\(\perp\)AE tại E
=>HE\(\perp\)AB tại E
Xét (O) có
ΔAFH nội tiếp
AH là đường kính
Do đó; ΔAFH vuông tại F
=>HF\(\perp\)FA tại F
=>HF\(\perp\)AC tại F
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
c: Ta có: ΔHEB vuông tại E
mà EM là đường trung tuyến
nên EM=HM
=>\(\widehat{MHE}=\widehat{MEH}\)
mà \(\widehat{MHE}=\widehat{ACB}\)(hai góc đồng vị, HE//AC)
nên \(\widehat{MEH}=\widehat{ACB}\)
Ta có: AEHF là hình chữ nhật
=>\(\widehat{FEH}=\widehat{FAH}\)
mà \(\widehat{FAH}=\widehat{ABC}\left(=90^0-\widehat{HCA}\right)\)
nên \(\widehat{FEH}=\widehat{ABC}\)
\(\widehat{MEF}=\widehat{MEH}+\widehat{FEH}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
Vì AEHF là hình chữ nhật
nên AEHF nội tiếp đường tròn đường kính AH và EF
=>EF là đường kính của (O)
Xét (O) có
EF là đường kính
EM\(\perp\)EF tại E
=>EM là tiếp tuyến của (O)


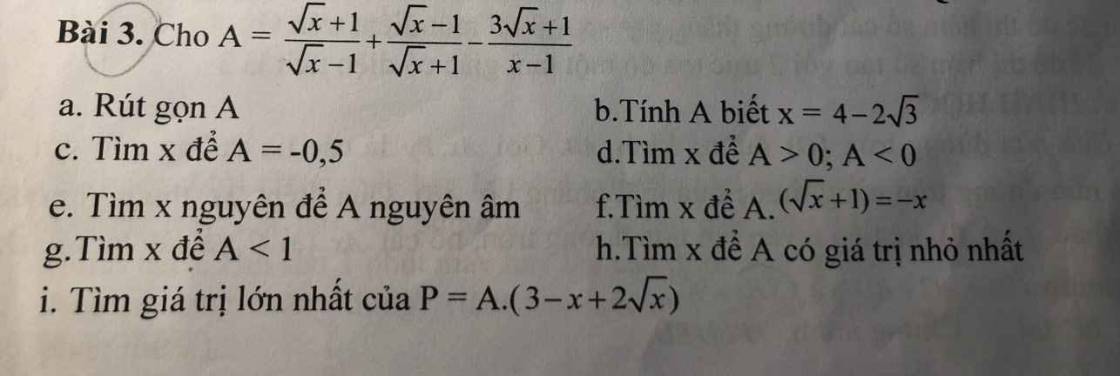 cíu cíu
cíu cíu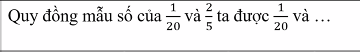

 cíu tui cíu tui
cíu tui cíu tui


 cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui
\(n_{AgNO_3}=1.0,5=0,5\left(mol\right);n_{HCl}=2.0,3=0,6\left(mol\right)\)
PTHH: AgNO3 + HCl → AgCl ↓ + HNO3
Mol: 0,5 0,5 0,5
Ta có: \(\dfrac{0,5}{1}< \dfrac{0,6}{1}\)⇒ AgNO3 pứ hết, HCl dư
* Vdd sau pứ = 0,5+0,6 = 1,1 (l)
\(\Rightarrow C_{M_{ddNO_3}}=\dfrac{0,5}{1,1}=0,4545M\)
\(C_{M_{ddHCldư}}=\dfrac{0,6-0,5}{1,1}=0,0909M\)
\(m_{ddAgNO_3}=500.1,2=600\left(g\right);m_{ddHCl}=300.1,5=450\left(g\right)\)
* mdd sau pứ = 600+450 = 1050 (g)
\(C\%_{ddHNO_3}=\dfrac{0,5.63.100\%}{1050}=3\%\)
\(C\%_{ddHCl}=\dfrac{\left(0,6-0,5\right).36,5.100\%}{1050}=0,348\%\)
Vdd sau pứ phải là 0,5 + 0,3 = 0,8 (l) (dòng 4) chứ bn.