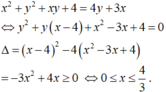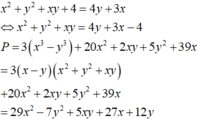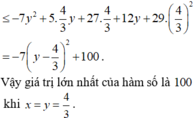Cho x>0, y>=0 thỏa mãn x3+y3=x-y. Tìm GTLN của biểu thức x2+y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x+y+4=0\Rightarrow\left\{{}\begin{matrix}y=-4-x\\x+y=-4\end{matrix}\right.\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=\left(-4\right)^3-3xy.\left(-4\right)=12xy-64\)
\(\Rightarrow P=2\left(12xy-64\right)+3\left(x^2+y^2\right)+10x\)
\(=24xy+3x^2+3y^2+10x-128\)
\(=24x\left(-4-x\right)+3x^2+3\left(-4-x\right)^2+10x-128\)
\(=-18x^2-62x-80=-18\left(x+\dfrac{31}{18}\right)^2-\dfrac{479}{18}\le-\dfrac{479}{18}\)
\(P_{max}=-\dfrac{479}{18}\) khi \(\left(x;y\right)=\left(-\dfrac{31}{18};-\dfrac{41}{18}\right)\)

\(x^3+y^3+3\left(x^2+y^2\right)+4\left(x+y\right)+4=0\)
\(\Leftrightarrow\left(x+y\right)^3-3xy\left(x+y\right)+3\left(x+y\right)^2-6xy+4\left(x+y\right)+4=0\)
\(\Leftrightarrow\left(x+y+2\right)\left(\left(x+y\right)^2+x+y+2\right)-3xy\left(x+y+2\right)=0\)
\(\Leftrightarrow\left(x+y+2\right)\left(x^2+y^2+2xy+x+y+2-3xy\right)=0\)
\(\Leftrightarrow\left(x+y+2\right)\left[\left(x-y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2+2\right]=0\)
\(\Leftrightarrow x+y+2=0\)
\(\Leftrightarrow x+y=-2\)
\(M=\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}=\frac{4}{-2}=-2\)
Dấu \(=\)khi \(x=y=-1\).

Ta cá:\(K=x^2-2\times x-y=x^2-\left(2\times x+y\right)\)
Để K đạt GTLN
Suy ra x^2 lớn nhất nên x lớn nhất
2x+y nhỏ nhất nên y nhỏ nhất(2x Ko nhỏ nhất vi x lớn nhất nên 2x lớn nhất)
Mà \(y\ge0\)
Ta chọn y=0,thay vào 2x+y ta đc
\(2\times x+0\le4\)
\(\Rightarrow2\times x\le4\)
\(\Rightarrow x\le2\)
Mà x lớn nhất nên ta chọn x=2 do đá k sẽ bằng
\(K=2^2-2\times2-0=4-4=0\)
Vậy K đạt GTLN là 0 tại x =2 và y=0
nhớ h cho mk nha

Sửa đề: \(P=x^{2008}+y^{2009}+z^{2010}\)
Ta có: x+y+z=1
nên \(\left(x+y+z\right)^3=1\)
\(\Leftrightarrow x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(x+z\right)=1\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(z+x\right)+1=1\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
mà 3>0
nên \(\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\x+z=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-y\\y=-z\\x=-z\end{matrix}\right.\)
Thay x=-y vào biểu thức \(x+y+z=1\), ta được:
\(-y+y+z=1\)
hay z=1
Thay x=-y và z=1 vào biểu thức \(x^2+y^2+z^2=1\), ta được:
\(\left(-y\right)^2+y^2+1=1\)
\(\Leftrightarrow y^2+y^2=0\)
\(\Leftrightarrow2y^2=0\)
hay y=0
Vì x=-y
và y=0
nên x=0
Thay x=0; y=0 và z=1 vào biểu thức \(P=x^{2008}+y^{2009}+z^{2010}\), ta được:
\(P=0^{2008}+0^{2009}+1^{2010}=1\)
Vậy: P=1
nma ở trên cm y=-z mà. Nếu ở thay y=0 và z=1 vào thì nghĩa là 0 = -1 hả