Cho hàm số y =2x/x+1 (C) tìm M thuộc(C) biết tiếp tuyến của C tại M cắt 2 trực ox và oy là A Và B diện tích tam giác OAB =1/4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 2 2018
Đáp án D
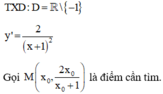
Phương trình đường tiếp tuyến ∆ tại M của (C) là
Giải phương trình bậc hai ta suy ra có hai điểm M thỏa mãn đề bài M(1;1) hoặc M - 1 2 ; - 2
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2021
\(y'=\dfrac{-3}{\left(x-1\right)^2}\)
Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\dfrac{-3}{\left(x_0-1\right)^2}\left(x-x_0\right)+\dfrac{2x_0+1}{x_0-1}\) (1)
a.
Tọa độ A và B có dạng: \(A\left(\dfrac{2x_0^2+2x_0-1}{3};0\right)\) ; \(B\left(0;\dfrac{2x_0^2+2x_0-1}{\left(x_0-1\right)^2}\right)\)
\(\Rightarrow OA=\left|\dfrac{2x_0^2+2x_0-1}{3}\right|;OB=\dfrac{\left|2x_0^2+2x_0-1\right|}{\left(x_0-1\right)^2}\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{6}\Rightarrow OA.OB=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{\left(2x_0^2+2x_0-1\right)^2}{3\left(x_0-1\right)^2}=\dfrac{1}{3}\Rightarrow\left(2x_0^2+2x_0-1\right)^2=\left(x_0-1\right)^2\)
\(\Leftrightarrow\left(2x_0^2+3x_0-2\right)\left(2x_0^2+x_0\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=0\\x_0=-\dfrac{1}{2}\\x_0=-2\\x_0=\dfrac{1}{2}\end{matrix}\right.\)
Có 4 tiếp tuyến thỏa mãn:... (thế lần lượt các giá trị \(x_0\) vào (1) là được)
CM
6 tháng 1 2017
Đáp án C
- Viết phương trình tiếp tuyến với C tại M.
+ Phương trình tiếp tuyến với đồ thị hàm số y = f x tại điểm M x 0 ; f x 0 :y=f ' x o x-x o +f x o .
- Tìm tọa độ hai giao điểm A,B của tiếp tuyến với các trục tọa độ Ox, Oy.
- Diện tích tam giác OAB là: S Δ O A B = 1 2 O A . O B .
y = 1 x ⇒ y ' = 1 x 2 . Ta có:
x M = 2 − 3 ⇒ y M = 1 2 − 3 = 2 + 3 ⇒ M 2- 3 ; 2 + 3 .
Phương trình tiếp tuyến với C tại M 2- 3 ; 2 + 3 là:
d : y = − y ' x M x-x M + y M = − 1 2 − 3 2 x − 2 + 3 + 2 + 3 = − 2 + 3 2 x + 4 + 2 3 .
Cho x = 0 ⇒ y = 4 + 2 3 ⇒ B 0;4+2 3
Cho
y = 0 ⇒ x = 4 + 2 3 2 + 3 = 2 2 + 3 = 4 − 2 3 ⇒ A 4 − 2 3 ; 0
Vậy S O A B = 1 2 O A . O B = 1 2 4 + 2 3 4 − 2 3 = 2 .
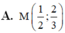
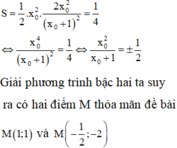
Lời giải:
Gọi tọa độ điểm \(M(a,\frac{2a}{a+1})\)
\(y=\frac{2x}{x+1}\Rightarrow y'=\frac{2}{(x+1)^2}\)
Do đó phương trình tiếp tuyến của $(C)$ tại $M$ là:
\((d):y=f'(a)(x-a)+f(a)=\frac{2}{(a+1)^2}(x-a)+\frac{2a}{a+1}\)
\(\Leftrightarrow (d):y=\frac{2x+2a^2}{(a+1)^2}\)
Do đó: \((d)\cap Ox=A(-a^2,0)\)
\((d)\cap (Oy)=B(0, \frac{2a^2}{(a+1)^2})\)
Có: \(S_{OAB}=\frac{OA.OB}{2}=\frac{|-a^2||\frac{2a^2}{(a+1)^2}|}{2}=\frac{1}{4}\)
\(\Leftrightarrow \frac{2a^4}{(a+1)^2}=\frac{1}{2}\)
\(\Leftrightarrow 4a^4-(a+1)^2=0\Leftrightarrow (2a^2-a-1)(2a^2+a+1)=0\)
Giải pt dễ dàng tìm được \(\left[\begin{matrix} a=1\\ a=\frac{-1}{2}\end{matrix}\right.\) (t/m)
Do đó \(M\in\left\{(1,1); (\frac{-1}{2}, -2)\right\}\)