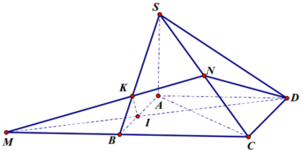
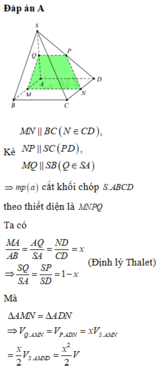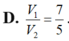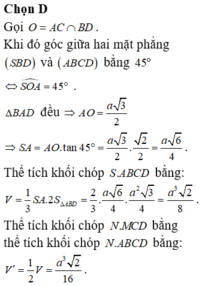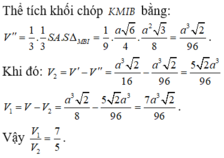Cho hình chóp SABCD có ABCD là hình bình hành. Gọi E,F là trung điểm AB, AD. Lấy điểm H trên SC sao cho SC=3SH. Mặt phẳng HEF chia hình chóp thánh 2 phần. Phần chứa điểm S có thể tích V1 phần còn lại có thể tích V2. Tính V1/V2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi P là giao điểm của mặt phẳng (EMN) với cạnh AB. Ta có ME là đường trung bình của tam giác SAB, nên ta có ME song song với đoạn thẳng AB và ME = 1/2 * AB. Tương tự, ta cũng có MN song song với cạnh SC và MN = 1/2 * SC. Vì EMN là tam giác đều, nên ta có EP = EN = NP = 1/3 * EMN.
Vì E là trung điểm của SA, nên ta có SE = 1/2 * SA. Vì SN là đường trung bình của tam giác SCA, nên ta có SN = 1/2 * SC.
Từ các thông tin trên, ta có thể xác định các điểm P, E, và N trên hình chóp S.ABCD. Sau đó, ta vẽ đường thẳng EN và vẽ đường thẳng qua P song song với đáy ABCD, giao điểm của hai đường thẳng này là điểm M.
Vậy, thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (EMN) là một hình bình hành có các đỉnh là các điểm E, M, N và các cạnh là các đoạn thẳng EM, MN, NE.


Gọi O là tâm hình bình hành; MN cắt AC tại J
Kẻ PE//SO thì E là trung điểm của OC suy ra \(IO=\frac{1}{2}PE=\frac{1}{4}SO\)
Gọi thể tích khối chóp là V
Ta có : \(\frac{V_{S.B'D'P}}{V_{S.BCD}}=\frac{SB'}{SB}.\frac{SD'}{SD}.\frac{SP}{SC}=\frac{3}{4}.\frac{3}{4}.\frac{1}{2}=\frac{9}{32}\)
suy ra \(V_{S.B'D'P}=\frac{9}{32}V_{S.BCD}=\frac{9}{64}V\)
Suy ra \(V_{BDD'BPC}=\frac{1}{2}V-\frac{9}{64}V=\frac{23}{64}V\)
pcm \(V_{MNDD'B'B}=\frac{9}{64}V\)
Ta có : \(V_{MNDD'B'B}=V_{J.BB'D'D}+V_{M.BB'J}+V_{N.DD'J}=V_{J.BB'D'D}+2.V_{M.BB'J}\)
Với \(V_{J.BB'D'D}=\frac{1}{2}V_{A.BB'D'D}=\frac{1}{2}\left[1-\left(\frac{3}{4}\right)^2\right].V_{A.SBD}\)\(=\frac{1}{2}.\frac{7}{16}.\frac{1}{2}V=\frac{7}{64}V\)
\(V_{M.BB'J}=V_{B'.BMJ}=\frac{1}{4}V_{S.BMJ}=\frac{1}{4}.\frac{1}{8}V_{S.ABD}\)\(=\frac{1}{4}.\frac{1}{8}.\frac{1}{2}V=\frac{1}{64}V\)
Vậy \(V_{MNDD'B'B}=V_{J.BB'D'D}+2.V_{M.BB'J}=\frac{7}{64}V+2\frac{1}{64}V=\frac{9}{64}V\left(đpcm\right)\)
Gọi H là khối đa diện nằm bên dưới mp(MNP)
Gọi h,S,V lần lượt là chiều cao, diện tích đáy, thể tích của khối chóp S.ABCD
Dễ thấy:
\(\hept{\begin{cases}S_{DNU}=S_{BMT}=S_{AMN}=\frac{1}{4}S_{ABD}=\frac{1}{8}S\\d\left(p;\left(ABCD\right)\right)=\frac{1}{2}h;d\left(q;\left(ABCD\right)\right)=d\left(r;\left(ABCD\right)\right)=\frac{1}{4}h\end{cases}}\)
Ta có: \(S_{CTU}=S+\frac{1}{8}S=\frac{9}{8}S\)
\(V_{P\cdot CTU}=\frac{1}{3}\cdot\frac{1}{2}h\cdot\frac{9}{8}S=\frac{9}{16}V\)
\(V_{Q\cdot UDN}=V_{R\cdot BMT}=\frac{1}{3}\cdot\frac{1}{4}\cdot\frac{1}{8}S=\frac{1}{32}V\)
\(V_H=V_{P\cdot CTU}-V_{Q\cdot UDN}-V_{R\cdot BMT}=\frac{1}{2}V\)
=> đpcm
Nguồn: Chú lùn thứ 8

Chọn đáp án D
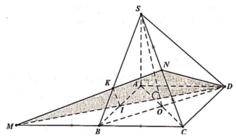
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
Thể tích khối chóp S.ABCD bằng: 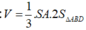
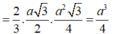
Ta có: N là trung điểm SC nên 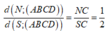
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
Ta có K là trọng tâm tam giác SMC
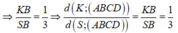

Thưa chị, em không vẽ hình vì sợ duyệt, với lại em lớp 9 nên chỉ làm bài này dựa vào chút kiến thức lớp 8 thôi ạ.
a) Hình bình hành ABCD có O là tâm nên O là trung điểm của đường chéo BD.
Xét \(\Delta BDS\)có I và O lần lượt là trung điểm của BS, BD
\(\Rightarrow\)IO là đường trung bình của \(\Delta BDS\)\(\Rightarrow\)IO//DS
Mà \(DS\in mp\left(SAD\right)\)nên IO//\(mp\left(SAD\right)\)(đpcm)
Em không làm được câu b ạ, em xin lỗi chị.