K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
KF
2
Những câu hỏi liên quan
28 tháng 1 2022
a: Sửa đề; AE vuông góc với Oy tại E, BF vuông góc với OA tại F
Xét ΔOEA vuông tại E và ΔOFB vuông tại F có
OA=OB
\(\widehat{EOA}\) chung
Do đó: ΔOEA=ΔOFB
b: Xét ΔBEA vuông tại E và ΔAFB vuông tại F có
BA chung
EA=FB
Do đó: ΔBEA=ΔAFB
Suy ra: \(\widehat{BAE}=\widehat{ABF}\)
NT
3 tháng 8 2021
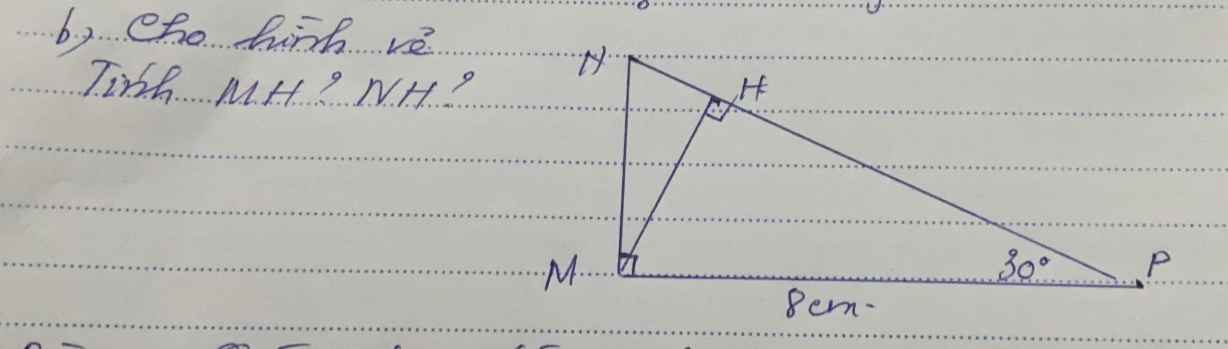
Áp dụng tỉ số lượng giác của góc nhọn vào \(\Delta MHP\), ta có:
\(\cos30\text{°}=\dfrac{MH}{8}\Rightarrow MH=8.\cos30\text{°}=4\sqrt{3}\left(cm\right)\)
Mặt khác, \(\text{∠}MNP=90\text{°}-30\text{°}=60\text{°}\)
Áp dụng tí số lượng giác của góc nhọn vào \(\Delta MHN\), ta có:
\(\tan60\text{°}=\dfrac{4\sqrt{3}}{NH}\Rightarrow NH=4\sqrt{3}.\tan60\text{°}=12\left(cm\right)\)
AH
Akai Haruma
Giáo viên
3 tháng 8 2021
Lời giải:
Xét tam giác $MHP$ vuông tại $H$ thì:
$\frac{MH}{MP}=\sin P=\sin 30^0=\frac{1}{2}$
$\Rightarrow MH=\frac{MP}{2}=4$ (cm)
Theo định lý Pitago:
$HP=\sqrt{MP^2-MH^2}=\sqrt{8^2-4^2}=4\sqrt{3}$
Theo hệ thức lượng trong tam giác vuông:
$MH^2=NH.HP$
$\Leftrightarrow 4^2=4\sqrt{3}.NH$
$\Leftrightarrow NH=\frac{4\sqrt{3}}{3}$ (cm)
PS
0
TP
23 tháng 8 2021
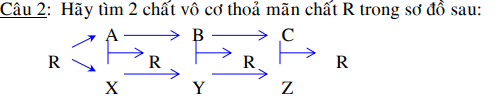
R là NaCl
A là Na, X là Cl2
B là NaOH, Y là HCl
C là Na2SO4, Z là BaCl2
\(NaCl-^{đpnc}\rightarrow Na+\dfrac{1}{2}Cl_2\)
\(Na+H_2O\rightarrow NaOH+\dfrac{1}{2}H_2\)
\(Cl_2+H_2-^{as}\rightarrow2HCl\)
\(NaOH+HCl\rightarrow NaCl+H_2O\)
\(2NaOH+H_2SO_4\rightarrow Na_2SO_4+2H_2O\)
\(2HCl+BaO\rightarrow BaCl_2+H_2O\)
\(BaCl_2+Na_2SO_4\rightarrow BaSO_4+2NaCl\)
DT
Đỗ Thanh Hải
CTVVIP
7 tháng 10 2021
1 B
2 B
3 C
4 B
5 C
6 C
7 C
8 B
9 D
10 C
11 A
12 A
13 A
14 D
15 B
16 B
17 A
18A
19 C
20 C
1N
1
NH
0
1. 168, 210
2.
3. Khỉ: 16 quả chuối
Voi: 4 quả chuối
4. 125, 25
~hok tot~
Chiều rộng bằng bao nhiêu phần chiều dài vậy