Một người đi xe đạp từ A và B cách nhau 20km trong một thời gian đã định. Sau khi đi được 1h với vận tốc dự định, người đó giảm vận tốc đi 2km/h trên quãng đường còn lại, nên đã đến B chậm 15 phút so với dự định. Tính vận tốc dự định của người đi xe đạp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 2 2019
đáp án là 10km/h
Gợi ý: ta có pt là
20/a + 1/4 = 1 + (20-a)/(a-2)
Trong đó:
a là vận tốc dự định
20/a là thời gian dự định
1/4 là 15p
(20-a)/(a-2) là thời gian đi trong quãng đường còn lại
Khai triển pt ta sẽ có:
4(a^2-40) = 3(a^2-2a)
<=>4a^2-160 = 3a^2 - 6a
<=>a^2 + 6a = 160
<=>a^2 + 6a - 160= 0
<=>a^2 + 16a - 10a - 160= 0
<=>a(a +16) - 10(a +16) = 0
<=>(a +16)(a -10) = 0
+Hoặc a +16 =0 <=> a= -16(loại vì vận tốc luôn luôn dương)
+Hoặc a -10 =0 <=> a= 10 (nhận)
Vậy vận tốc dự định của người đi xe đạp là 10km/h
CM
20 tháng 8 2019
Gọi vận tốc dự định đi của người đó là x (km/h) (x > 0)
Thời gian dự định đi của người đó là 36/x (h)
Thời gian người đó đi nửa quãng đường đầu là 18/x (h)
Nửa quãng đường sau người đó đi với vận tốc là x + 2 (km/h) và thời gian người đó đi là 18/(x+2) (h)
Vì nghỉ lại 30 phút nên thời gian đi từ lúc xuất phát đến khi tới B là 18 x + 1 2 + 18 x + 2
Do người đó đến B chậm hơn dự kiến 12 phút = 1/5h nên ta có phương trình:
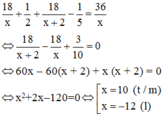
Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB là 12 km/h
Đáp án: A
2 tháng 12 2023
Gọi vận tốc dự định của người đi xe đạp là x(km/h)
(Điều kiện: x>0)
Thời gian dự kiến sẽ đi hết quãng đường là \(\dfrac{20}{x}\left(h\right)\)
Vận tốc sau khi giảm đi 2km/h là:
x-2(km/h)
Sau 1h thì xe đạp đi được: 1*x=x(km)
Độ dài quãng đường còn lại là 20-x(km)
Thời gian thực tế đi hết quãng đường là:
\(1+\dfrac{20-x}{x-2}\left(h\right)\)
Vì người đó đi chậm hơn dự định 30p=0,5h nên ta có:
\(1+\dfrac{20-x}{x-2}-\dfrac{20}{x}=0,5\)
=>\(\dfrac{20-x}{x-2}-\dfrac{20}{x}=\dfrac{-1}{2}\)
=>\(\dfrac{x\left(20-x\right)-20\left(x-2\right)}{x\left(x-2\right)}=\dfrac{-1}{2}\)
=>\(\dfrac{20x-x^2-20x+40}{x\left(x-2\right)}=\dfrac{-1}{2}\)
=>\(\dfrac{x^2-40}{x\left(x-2\right)}=\dfrac{1}{2}\)
=>\(2\left(x^2-40\right)=x\left(x-2\right)\)
=>\(2x^2-80-x^2+2x=0\)
=>\(x^2+2x-80=0\)
=>\(\left(x+10\right)\left(x-8\right)=0\)
=>\(\left[{}\begin{matrix}x+10=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-10\left(loại\right)\\x=8\left(nhận\right)\end{matrix}\right.\)
Vậy: vận tốc dự định là 8km/h
Gọi x ( km/h ) là vận tốc dự định của người đó
( x > 0 )
+ Thời gian người đó dự định đi hết QĐ AB là :
\(\frac{20}{x}\) ( h )
Trong 1 h người đó đi đc : x ( km)
+ Vận tốc của người đó trên QĐ còn lại là :
x - 2 ( km/h )
Quãng đg người đó đi vs vận tốc x - 2 km/h là :
20 - x ( km )
Thời gian người đó đi 20 - x ( km ) còn lại là :L
\(\frac{20-x}{x-2}\) ( h )
+ Ta có pt : \(\frac{20-x}{x-2}+1-\frac{20}{x}=0,25\)
\(\Leftrightarrow\frac{x\left(20-x\right)+x\left(x-2\right)-20\left(x-2\right)}{x\left(x-2\right)}=\frac{1}{4}\)
\(\Leftrightarrow4\left(40-2x\right)=x^2-2x\)
\(\Leftrightarrow x^2+6x-160=0\)
\(\Leftrightarrow\left(x-10\right)\left(x+16\right)=0\)
\(\Leftrightarrow x=10\) ( TM )
Vậy vận tốc dự định của người đi xe đạp là 10 km/h