Rút gọn biểu thức : P=\(\dfrac{1+sin6x-cos6x}{1+sin6x+cos6x}\) sau đó tính P khi x= \(\dfrac{7\pi}{4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\dfrac{-2sin5x.sinx-sinx}{2sin5x.cosx+cosx}=\dfrac{-sinx\left(2sin5x+1\right)}{cosx\left(2sin5x+1\right)}=-tanx\)

Chọn B.
Ta có A = sin6x + cos6x + 3sin2x.cos2x.
= ( sin2x)3 + (cos2x)3 + 3sin2x.cos2x.
= (sin2x + cos2x)3 - 3sin2x.cos2x(sin2x + cos2x) + 3.sin2x.cos2x
= 1 - 3.sin2x.cos2x + 3.sin2x.cos2x = 1

\(A=3\left[\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\right]-2\left[\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)\right]\)
\(=3\left[1-2\cdot sin^2x\cdot cos^2x\right]-2\left[1-3\cdot sin^2x\cdot cos^2x\right]\)
\(=3-6\cdot sin^2x\cdot cos^2x-2+6\cdot sin^2x\cdot cos^2x\)
=1

a, Ta có: sin 4 x + cos 4 x = sin 2 x + cos 2 x 2 - 2 sin 2 x . cos 2 x = 1 - 2 sin 2 x . cos 2 x
b, Ta có: sin 6 x + cos 6 x = sin 2 x + cos 2 x 3 - 3 sin 2 x cos 2 x sin 2 x + cos 2 x = 1 - 3 sin 2 x cos 2 x

Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.
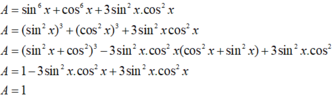
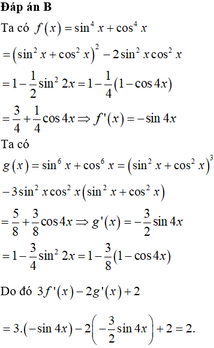
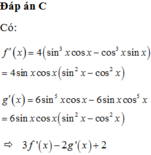
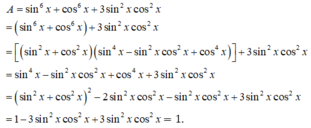
\(P=\dfrac{1+2sin3xcos3x-\left(1-2sin^23x\right)}{1+2sin3xcos3x+2cos^2x-1}=\dfrac{2sin3xcos3x+2sin^23x}{2sin3xcos3x+2cos^23x}=\dfrac{sin3x}{cos3x}=tan3x\)
\(x=\dfrac{7\pi}{4}\Rightarrow P=tan\dfrac{21\pi}{4}=tan\dfrac{\pi}{4}=1\)