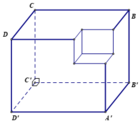
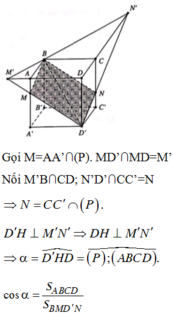một khối lập phương lớn được tạo bởi 27 khối lập phương đơn vị.Một mặt phẳng vuông góc với đường chéo của khối lập phương lớn tại trung điểm của nó.Mặt phẳng này cắt ngang(không đi qua đỉnh)của bao nhiêu khối lập phương đơn vị
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 9 2017
Đáp án D
Giả sử các đỉnh của khối lập phương đơn vị là (i;j;k) với i;j;k ∈ {0;1;2;3}và đường chéo đang xét của khối lập phương lớn nối hai đỉnh O(0;0;0) và A(3;3;3)
Phương trình mặt phẳng trung trực OA là (α): x + y + x – 9 2 = 0
Mặt phẳng này cắt khối lập phương đơn vị khi các đầu mút (i;j;k) và (i+1;j+1;k+1) của đường chéo của khối lập phương đơn vị nằm về hai phía đối với (α). Do đó bài toán quy về đếm trong số 27 bộ (i;j;k), với bộ số i;j;k ∈ {0;1;2}thỏa mãn
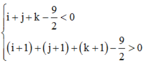
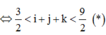
Các bộ 3 không thỏa mãn điều kiện (*) là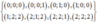 
Do đó có 27 – 8 =19 khối lập phương đơn vị bị cắt bởi (α)
25 tháng 5 2020
Thể tích phần cưa tại mỗi đỉnh là:
\(\frac{1}{3}.6.\left(\frac{1}{2}.6.6\right)=36\left(cm^3\right)\)
Vì có 8 đỉnh nên thể tích bị cắt đi là:
36 . 8 = 288 ( cm3 )
Thể tích khối gỗ là:
123= 1728 (cm3 )
Thể tích phần còn lại là:
1728 - 288 = 1440 (cm^3)
CM
31 tháng 7 2018
Chọn D.
Để khối lập phương nhỏ thu được sau khi cắt có có đúng 2 mặt được sơn đỏ thì khối lập phương nhỏ đó phải có một cạnh nằm trên cạnh giao của hai mặt hình lập phương, mà tại các đỉnh thì khối lập phương nhỏ thu được sẽ có 3 mặt được tô đỏ.
=> trên một cạnh của hình lập phương ta sẽ có có 8 khối lập phương nhỏ thỏa mãn đề. Vì hình lập phương có tất cả 12 cạnh nên số khối lập phương thu được sau khi cắt có đúng 2 mặt được sơn đỏ là 8.12=96.
CM
2 tháng 2 2019
Chọn B
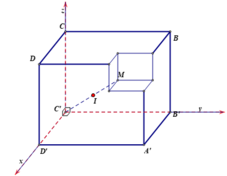
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC' và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa yêu cầu bài toán.
Suy ra I thuộc đoạn thẳng C'M và mặt cầu tâm I cần tìm đi qua điểm M
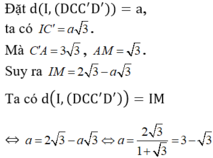
Cách khác: Chọn hệ trục tọa độ Oxyz sao cho C'(0;0;0), B' (0;3;0), D'(3;0;0), C (0;0;3).
Khi đó M(2;2;2)
Ta có phương trình đường thẳng C'M là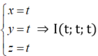 
với 2 > 0 > t do I thuộc đoạn thẳng C'M
